공통수학 1 💡시험 기간 필수 복습💡 RPM 13p 62번 문제 풀이 & 해설 - 곱셈 공식의 변형

📌 문제 : 공통수학 1 RPM 13p 62번

이 글은 공통수학 1의 핵심 개념인 곱셈공식 응용 문제를 다룹니다.
해당 문제는 합의 제곱, 곱의 항등식을 기반으로 하며, 복잡해 보이는 식도 기본 공식으로 빠르게 해결할 수 있는 구조입니다.

 

"이 블로그는 RPM 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."

---

🧠 문제 요약

$a + b + c = 4, a^2 + b^2 + c^2 = 14, abc = -6$

$a^2b^2 + b^2c^2 + c^2a^2$의 값은?

 

🔍  해설 요약

• 식을 $a^2b^2 + b^2c^2 + c^2a^2 = (ab)^2 + (bc)^2 + (ca)^2$ 꼴로 보기
• $(x + y + z)^2 = x^2 + y^2 + z^2 + 2(xy + yz + zx)$ 공식을 이용

---

✏️  풀이 과정

Step 1. 

구하고자 하는 식을 먼저 보면

 

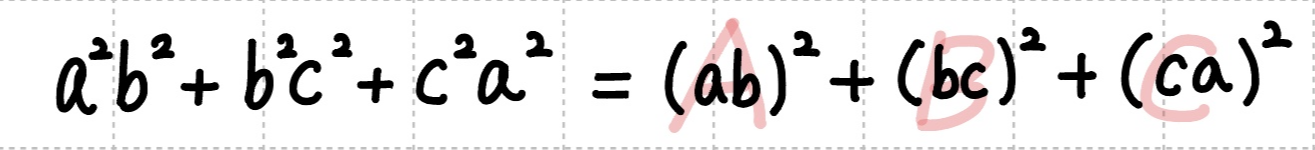
$A^2 + B^2 + C^2 = (A + B + C)^2 - 2(AB + BC + CA)$ 공식을 이용하는데, 천천히 괄호를 이용해 정리해 줍니다. 

 

주어진 $a + b + c = 4$, $abc = -6$이므로 $ab + bc + ca$의 값만 구해주면 됩니다.

 

---

Step 2. $ab + bc + ca$ 값 구하는 과정

$(a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca)$

$16 = 14 + 2(AB + BC + CA)$

$ herefore ab + bc + ca = 1$

---

Step 3. 최종계산 

$(ab)^2 + (bc)^2 + (ca)^2 = (ab + bc + ca)^2 - 2abc(a + b + c)$

$= (1)^2 - 2(-6)(4)$

$= 1 + 48$

$= 49$

 

---

✅ 정답: 49

💡 Tip

식의 구조를 보고 $A^2 + B^2 + C^2 = (A + B + C)^2 - 2(AB + BC + CA)$를 떠올리는 과정이 핵심입니다. 

또한, 계산 실수가 많은 학생이라면 식을 정리할때 위에 기본 공식을 써두고 차근차근 적어보는 연습을 하도록 합시다. 

📎 관련 문제

• 곱셈공식의 변형 - 개념원리 25p 필수예제 09