
1 단원 - 2. 항등식과 나머지 정리 - 항등식과 방정식
고등학교 수학에서 항등식과 방정식은 필수 개념입니다. 방정식은 특정 값에서만 성립하는 해를 찾는 것이 목적이지만, 항등식은 모든 값에 대해 항상 성립하는 식입니다. 이를 효과적으로 풀이하기 위해 미정계수법의 계수비교법과 수치대입법을 이해하는 것이 중요합니다.
이번 글에서는 개념원리 교재 예제 문제를 통해 항등식과 방정식의 차이를 설명하고, 실제 시험에서 자주 출제되는 유형별 풀이법을 소개합니다. 각 방법의 장단점을 비교하며 학습하면 수능 및 내신 대비에 도움이 될 것입니다.
개념원리 공통수학 1 : 38p ~ 42p
"모바일 접속 시 함수가 보이지 않을 수 있습니다. 태블릿이나 컴퓨터 또는 chrome(크롬)을 이용해 접속해 주세요."
배울 내용 요약
방정식
- $2x - 1 = 3$ $\Rightarrow x = 2$
- 특정 $x$에 대해서만 성립
- 목적: 특정 $x$를 구하는 것 (즉, 해를 구하는 것)
항등식
- $2x - 1 = ax - 1$ $\Rightarrow a = 2$
- " 어떤 $x$ 값에 대하여도, 모든 $x$에 대해서, 임의의 $x$에 대해서, $x$에 관계없이 " 성립
- 목적: 식을 항등식으로 만들어 주는 것
- "미정계수법"
- 계수비교법: 양변의 동류항 계수 비교 - 항등식 성질 이용
- 수치대입법: 적당한 수를 대입하여 값이 같음을 이용 - 항등식 정의를 이용
- "미정계수법"
1. 항등식과 방정식
방정식의 목표는 '식을 만족하는 근,해 구하는 것이 목표' 라면, 항등식은 '좌변과 우변을 같은 식으로 만들어 주는 것이 목표' 입니다.
방정식의 $2x - 1 = 3$
- $x$에 3을 대입했을 때 성립하지 않습니다.
- $x$에 4를 대입해도 성립하지 않습니다.
- $x$에 2를 대입했을 때만 성립합니다.
- 즉, 특정 값에서만 식을 만족하고 이를 만족하는 $x$값을 구하는 것이 목표이자 답
항등식은 문자에 어떤 값을 넣어도 '항'상 성립하는 '등식'을 보고 항등식이라고 합니다. 그렇다면 좌변과 우변의 식이 같아야 항상 값도 같고 등식도 성립하겠죠?
항등식의 $2x - 1 = ax - 1$
- 좌변과 우변의 식이 같아지게 우변의 $x$의 계수 $a$를 2로 만들어주면 된다.
- $2x - 1 = 2x - 1$ 로 식이 같아지면 $x$에 1을 대입하든, 2를 대입하든 항상 성립
- 즉, 어떤 $x$ 값에 대하여도, 모든 $x$에 대해서, 임의의 $x$에 대해서, $x$에 관계없이 성립한다
2. 항등식의 성질
그래서 나오는 항등식의 성질로는
- $ax^2 + bx + c = a'x^2 + b'x + c'$ 이 $x$에 대한 항등식
- ↑↓ 각각의 계수가 같아야 하므로
- $a = a', b = b', c = c'$
- $ax^2 + bx + c = 0$ 이 $x$에 대한 항등식
- 0을 좌변의 꼴과 같게 생각해주면, $ax^2 + bx + c = 0x^2 + 0x + 0$
- ↑↓ 각각의 계수가 같아야 하므로
- $ a = 0, b = 0, c = 0$
이렇게 계수를 맞춰 좌변과 우변의 식이 같도록 해주면 됩니다.
결론/정리 :
항등식의 정의 : 문자에 어떤 값을 넣어도 항상 성립하는 등식
항등식의 성질
① $ax^2 + bx + c = 0$이 $x$에 대한 항등식 $\Leftrightarrow a = 0, b = 0, c = 0$
② $ax^2 + bx + c = a'x^2 + b'x + c'$이 $x$에 대한 항등식 $\Leftrightarrow a = a', b = b', c = c'$
아직 조금 헷갈린다면 단순하게 말하자면 방정식과 항등식의 차이는 방정식은 $x$ 값을 구하는 것이라면, 항등식은 계수를 구하는 것 입니다.
3. 항등식에서의 "기준문자"
어떤 $x$ 값에 대하여도/ 모든 $x$에 대해서/ 임의의 $x$에 대해서/ $x$에 관계없이 성립하는
$\Rightarrow "x에 대한 항등식" $
어떤 $k$ 값에 대하여도/ 모든 $k$에 대해서/ 임의의 $k$에 대해서/ $k$에 관계없이 성립하는
$\Rightarrow "k에 대한 항등식" $
어떤 $x, y$ 값에 대하여도/ 모든 $x, y$에 대해서/ 임의의 $x, y$에 대해서/ $x, y$에 관계없이 성립하는
$\Rightarrow "x, y에 대한 항등식" $
이렇게 어떤 문자를 기준으로 봐주는지에 따라 같은 식이여도 답이 달라질 수 있습니다.
예를 들어, $kx + y = 0$ 이라는 식에서 기준문자를 바꿔가며 풀어보도록 하겠습니다.
- $x$에 대한 항등식으로 보는 경우
$x$를 문자로, 다른 이외의 것은 다 상수로 보기 ( 즉, $k, y$는 상수 취급) $\Rightarrow x$ 의 계수비교
0을 $0x + 0$으로 볼 수 있음
$\Rightarrow kx + y = 0x + 0$
$\therefore k = 0 , y = 0$
- $k$에 대한 항등식으로 보는 경우
$k$를 문자로, 다른 이외의 것은 다 상수로 보기 ( 즉, $x, y$는 상수 취급) $\Rightarrow k$ 의 계수비교
0을 $0k + 0$으로 볼 수 있음
$\Rightarrow xk + y = 0k + 0$
$\therefore x = 0 , y = 0$
이처럼, 같은 식이더라도 어떤 문자를 기준 문자로 보냐에 따라 답이 달라 질 수 있으니 무조건 $x$의 계수만 비교하지 않도록 합시다.
4. 미정계수법
항등식을 푸는 방법은 "정해지지 않은(미정) 계수를 구하는 법 : 미정계수법"을 이용합니다.
미정계수법에는 두가지가 있습니다.
1. 계수비교법 : 좌변과 우변의 식이 같아야 한다는 항등식의 성질을 이용해서 동류항의 계수를 비교하는 방법
2. 수치대입법 : 문자에 어떤 값을 넣어도 성립한다는 항등식의 정의를 이용해서 계수를 구하는 방법
아래의 예제 문제를 보면서 두가지 방법을 비교해 보도록 하겠습니다.
5. 예제 문제
항등식과 방정식 문제는 고등 수학 내신과 수능 대비에서 필수적으로 다루는 유형입니다. 예제별 풀이를 통해 항등식 문제 해결 전략을 배워 시험에 자주 출제되는 핵심 유형을 쉽게 이해할 수 있습니다. 빠르고 정확한 풀이를 위해 다양한 접근법을 비교하며 학습해 보세요!
설명할 문제 : 개념원리 41p 필수예제01, 개념원리 42p 필수예제02
개념원리 41p 필수예제01 (1)
풀이1. 계수비교법 이용
전개하여 동류항 계수를 비교해 줍니다.

전개할 때 부터 이렇게 동류항끼리 세로로 정리해가며 전개해주면 나중에 계산이 편리하답니다.
여튼, 전개해주고 각 동류항의 계수를 비교해주면
$a - 1 = b$, $-3 - a = -2$, $3 = c$
$\therefore a = -1, b = -2, c = 3$
풀이2. 수치대입법 이용
항등식은 기준문자에 어떤 값을 넣어도 성립한다는 점을 이용한 방법입니다.
아무값이나 넣어도 성립하는 것은 맞지만 그래도 어느수를 넣냐에 따라 계산이 복잡할 수도 있고 편리할 수도 있습니다.
예1)
$x = 100$ 대입 $\to$ $99 \left(100^2 + 100a - 3 \right) = 100^3 + 100^2b - 200 + C$
$\to$ 계산이 복잡
예2)
$x = 0$ 대입 시, 우변은 $c$만 남게 됩니다.
$\to$ $(-1)(-3) = c $
$\to$ $c = 3 $
$c$의 값을 바로 구하기 가능
답은 결국 같게 나오겠지만, 이렇게 어떤 값을 대입하냐에 따라 풀이가 복잡할수도, 편리할 수도 있습니다.
저는 아래와 같이 값을 대입해 주었지만, 다른 값을 넣어서 풀었다고 해서 잘못된 풀이 인것은 아닙니다.
최종 풀이 :
$x = 0$ 대입 $\to$ $(-1)(-3) = c $ $\therefore c = 3$
$x = 1$ 대입 $\to$ $(x - 1) = 0$에 의해 좌변 통째로 $0$됨
$0 = 1 + b - 2 + c$ $\therefore b = -2$
$x = -1$ 대입
$-2(1 - a - 3) = -1 + b + 2 + c$ $\therefore a = -1$
최종답 : $\therefore a = -1, , b = -2, , c = 3$
개념원리 41p 필수예제01 (2)
풀이1. 계수비교법 이용
전개하여 동류항 계수를 비교해 줍니다.
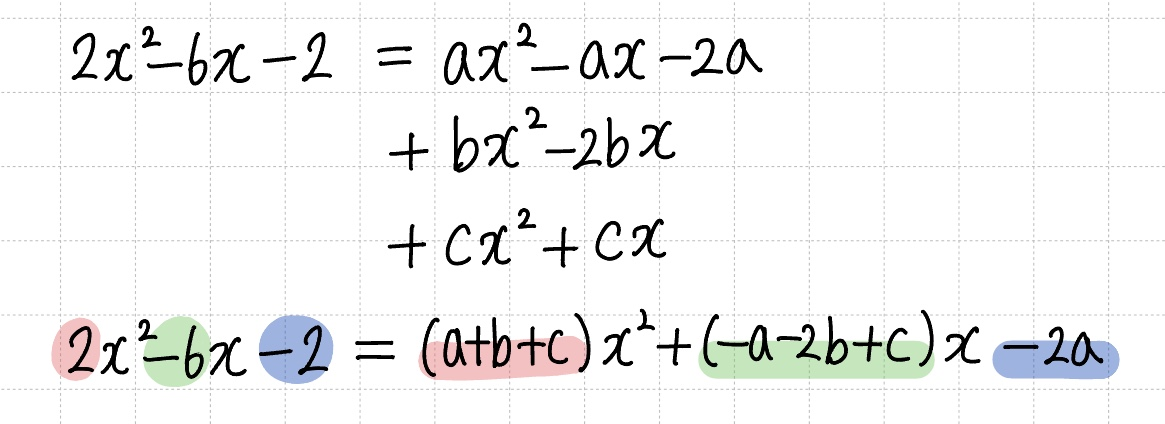
- $a + b + c = 2$, $-a - 2b + c = -6$, $-2a = -2$
- 세 번째 식에 의해 $a = 1$이라는 결론
- 첫 번째, 두 번째 식을 $a = 1$로 대입하여 정리 후 연립

$\therefore a = 1$, $b = 2$, $c = -1$
풀이2. 수치대입법 이용
적당한 수를 넣어가며 값이 같음을 이용해 줍니다.
주어진 식을 보면
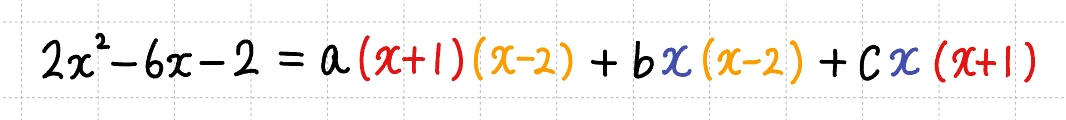
$(x+1), (x-2), x$가 반복되는 것을 알 수 있습니다.
- $x = 0$ 대입 시 $x$를 포함한 항 사라지고 $a$ 관련식 남음
- $-2 = a(1)(-2) + 0 + 0 \Rightarrow a = 1$
- $x = -1$ 대입 시 $x+1$을 포함한 항 사라지고 $b$ 관련식 남음
- $2 + 6 - 2 = 0 + b(-1)(-3) + 0 \Rightarrow b = 2$
- $x = 2$ 대입 시 $x-2$를 포함한 항 사라지고 $c$ 관련식 남음
- $8 - 12 - 2 = 0 + 0 + c(2)(3) \Rightarrow c = -1$
최종 결론 : $\therefore a = 1$, $b = 2$, $c = -1$
미정계수법 문제는 계수비교법과 수치대입법 중 하나를 선택해 풀이합니다.
- 반복되는 항이 있는 경우: 수치대입법이 편리한 경우가 많습니다.
- 반복되는 항이 없거나 전개가 간단한 식: 계수비교법을 사용하면 더 빠릅니다.
단, 모든 문제에 동일하게 적용되는 것은 아니며, 문제 유형에 따라 풀이법을 선택해야 합니다. 두 가지 방법을 모두 연습해 보며 자신에게 익숙한 방법을 찾는 것이 중요합니다.
미정계수법 요약/정리
1. 계수비교법
- 전개하여 양변의 동류항 계수 비교
- 좌변 우변 식 같게 (항등식 성질 이용)
- 반복되는 꼴이 없거나 전개가 쉬운 식에서 사용
2. 수치대입법
- 적당한 수를 대입하여 값이 같음을 이용
- 문자에 어느값을 넣어도 성립 (항등식 정의를 이용)
- 반복되는 꼴이 있는 경우 사용
개념원리 42p 필수예제02 (1)
문제에서 "등식 ~ 이 k의 값에 관계없이 항상 성립할 때" 라는 멘트가 나왔습니다. 그렇다면 $k$에 대한 항등식 이라고 생각할 수 있는데 항등식은 좌변과 우변의 식을 같게 해줘야 하기 때문에 기준문자 k 기준 내림차순 정리를 해서 각 항의 계수를 비교해주면 됩니다.

정리하자면, 위의 4가지 멘트가 나오면 " 기준문자에 대한 항등식이구나 " 생각 후 바로 " 기준문자에 대해 내림차순 정리 해보자 " 이렇게 바로 나와야 합니다.
문제의 주어진 식을 k에 대해 내림차순 정리를 해줄텐데, 저의 경우 속도를 좀 더 빠르게 하기 위해 아래와 같은 방법으로 식을 빠르게 정리하도록 합니다.
1. 식을 보고 기준문자의 최고차수를 판단한다.
이 문제에서는 기준문자 k의 최고 차수는 1
2. 내림차순 정리 틀을 먼저 만들어 준다.
이 문제에서는 k 최고 차수가 1이므로 ( 비워두기 )$k$ + ( 비워두기 ) = 0 틀 만들어 두기
ex) k의 최고 차수가 2인경우 ( 비워두기 )$k^2$+ ( 비워두기 )$k$ + ( 비워두기 ) = 0 틀 만들어 두기
3. 이후 차례로 전개하면서 괄호안에 바로바로 적기

주어진 식을 눈으로 차례 대로 전개하면서
머리로 $2kx$ 생각 -> (k 있으니) 첫번째 괄호에 $2x$ 적기
머리로 $-x$ 생각 -> (k 없으니) 두번째 괄호에 $-x$ 적기
머리로 $ky$ 생각 -> (k 있으니) 첫번째 괄호에 $y$ 적기
...
이렇게 바로바로 내림차순 정리 꼴로 적어줍니다. 그냥 전개해서 정리하셔도 되고 굳이 이 방법으로 하실 필요는 없지만 조금이나마 도움이 되었으면 하는 바램으로 적어봅니다. 조금 익숙해 지면 속도 정확성 다 잡을 수 있으니 연습해보는 것도 좋을 것 같아요.
이후, 우변의 0의 경우 $0k+0$으로 볼 수 있으므로 계수비교법을 이용하면, $2x + y - 1 = 0$, $-x + y - 7 = 0$
미지수가 2개고 식도 2개이므로 연립해주면 각각의 $x$, $y$값을 구할 수 있습니다.
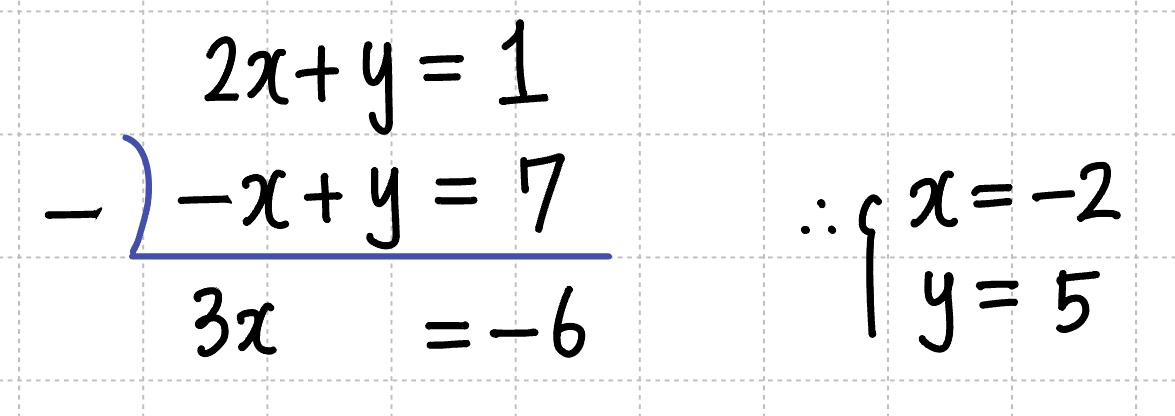
최종 결론 : $\therefore x = -2$, $y = 5$
개념원리 42p 필수예제02 (2)
문제에서 "모든 실수 $x, y$" 멘트가 나왔습니다.
$\Rightarrow x, y$에 대한 항등식
$\Rightarrow x, y$에 대해 내림차순 정리
- $x, y$의 최고차가 각각 1차이므로 $\rightarrow (\text{비워두기})x + (\text{비워두기})y + (\text{비워두기}) = 0$ 틀 만들고 바로 넣기

- $(a-b+2)x + (-2a+3b-3)y = 0$ 의 식으로 정리 됩니다.
- 우변이 $0$인 경우 $0 \cdot x + 0 \cdot y$로 볼 수 있습니다.
- $(a-b+2)x + (-2a+3b-3)y = 0 \cdot x + 0 \cdot y $
- 계수 비교법을 이용하여 $x, y$ 계수를 같게 해주면
- $a-b+2 = 0$, $-2a+3b-3 = 0$
미지수 $a, b$ 2개, 식 2개이므로 연립해주면 $a, b$ 값을 구할 수 있습니다.
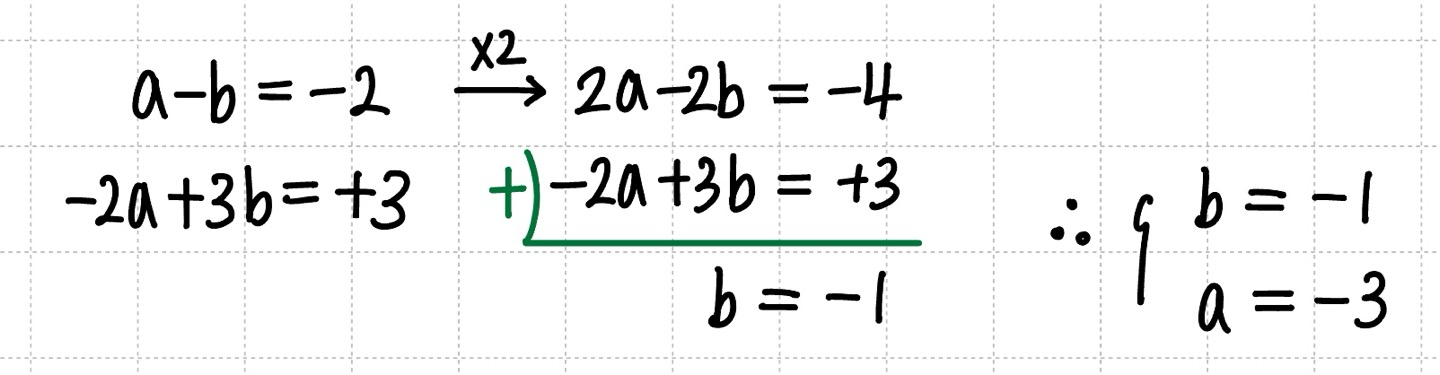
최종 결론 : $\therefore a = -3$, $b = -1$
6. 추가자료
개념 정리 자료 (한글파일 / pdf)
이 파일로 수업내용을 한번 간단하게 핵심 요약 정리를 해보시고 백지테스트를 해보도록 합시다.
"추가로 필요한 자료/ 문제에 대한 다른 풀이방법/ 글을 읽다 궁금한 점은 댓글로 남겨주세요!"
"이 블로그는 개념원리 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."
'공통수학 1 개념' 카테고리의 다른 글
| 공통수학 1 - 1 - 10. 항등식과 나머지 정리 - 확인체크, 연습문제 풀이 (0) | 2025.01.19 |
|---|---|
| 공통수학 1 - 1 - 9. 항등식과 나머지 정리 - 다항식의 나눗셈과 항등식 (4) | 2025.01.18 |
| 공통수학 1 - 1 - 7. 다항식의 연산 RPM 주요 문제 풀이 (4) | 2025.01.13 |
| 공통수학 1 -1 - 6. 다항식의 연산 확인체크 - 연습문제 풀이 (2) | 2025.01.11 |
| 공통수학 1 - 1 - 5. 다항식의 연산 - 다항식의 나눗셈 (3) | 2025.01.09 |



