
1단원 - 2. 항등식과 나머지 정리
항등식과 나머지 정리는 다항식 문제 풀이의 핵심 개념으로, 수능과 내신 대비에서 반드시 알아야 할 내용입니다. 이 글에서는 나머지 정리와 인수 정리를 중심으로 개념을 문제 풀이에 적용하는 과정을 소개하고 다양한 풀이를 함께 다룹니다.
"모바일 접속 시 함수가 보이지 않을 수 있습니다. 태블릿이나 컴퓨터 또는 chrome(크롬)을 이용해 접속해 주세요. "
개념원리 공통수학 1 : 52p ~ 54p
수에서의 나눗셈에 대한 등식

참고 :) 나눗셈에 대한 등식 : "(주어진 식) = (나누는 식)(몫) + (나머지)"
이 관점을 수에서도 적용시켜 해석해 보도록 할께요.
$ 8 = 3 \cdot 1 + 5 $
값으로는 당연히 성립하지만 "8을 3으로 나누었을 때 몫은 1 , 나머지가 5다."라는 나눗셈에 대한 등식 관점으로 보게 되면 틀린식이 됩니다.
왜 ? 나머지보다 나누는 수가 크기 때문이죠.
그렇다면 왜 크면 안될까요? 한번 더 나눠지기 때문입니다. (나머지를 나누는 수로 한번 더 나눌 수 있기 때문입니다.)
그래서 나머지를 나누는 수로 한번 더 나눠주게되면

$8 = 3 \cdot 1 + $ $ 5 $
- 나머지를 나누는 수로 나온 결과를 넣어 줍니다.
$= 3 \cdot 1 + $ $ 3 \cdot 1 + 2 $
- 나누는 수 3으로 묶어 정리해 줍니다.
$= 3 \cdot (1 + 1) + 2 $
$= 3 \cdot 2 + 2$
- 이제, " (나누는 수) $ \cdot $ (몫)+(나머지) " 관점으로 보면 식이 맞게 됩니다.
마찬가지로, 식에서도 (나누는 식의 차수) > (나머지 식의 차수) 조건을 만족해야 합니다.
왜? "한번 더 나눠지기 때문에 ! "
1. 예제 문제
개념원리 52p 발전예제07 - 삼차식으로 나누는 경우
이제 본격 문제 풀이에 들어가보도록 하겠습니다.
문제를 읽으며 주어진 조건이 무엇인지 식을 써줍니다.
$f(x) = (x-1)^2Q(x) + 3x + 2 \quad \dots \quad f(1) = 5$
$f(x) = (x+1)Q'(x) + 3 \quad \dots \quad f(-1) = 3$
$f(x) = (x-1)^2(x+1)Q''(x) + ax^2 + bx + c $
구해야 하는 것은 나머지 $ ax^2 + bx + c $ 입니다.
$f(1) = a + b + c = 5$
$f(-1) = a - b + c = 3$
미지수 $a, b, c$ 3개, 식 2개 $\Rightarrow$ 연립해도 $a, b, c$ 값을 구할 수 없게 됩니다.
그래서, '나누는 식' 관점 바꿔볼 것입니다.
원래 $(x-1)^2(x+1)$이 나누는 식인데 $(x-1)^2$을 나누는 식으로 본다면 나머지가 $3x + 2$가 되어야겠죠.
$f(1) = 5$ 값만 이용하지 않고 $f(x)$를 $(x-1)^2$으로 나누었을 때 나머지 $ 3x + 2 $를 통째로 이용하려는 것이죠.

$(x-1)^2$를 나누는 식으로 보면 나누는 식이 2차인데 나머지도 2차라서 잘못된 식이죠?
왜? 나머지가 $(x-1)^2$로 한 번 더 나눠지기 때문에 $\Rightarrow$ 한 번 더 나눠보자!!
나누는식 관점을 바꿔줄때는 꼭 나누는식의 차수와 나머지의 차수를 꼭 확인해 줘야합니다.
나머지를 $(x-1)^2$으로 나눠준 식
$ax^2 + bx + c = (x-1)^2 \cdot a + \boxed{\text{나머지 일차 이하}}$
- 좌변의 최고차 계수가 $a$ 이므로 우변도 최고차계수를 맞춰주면 몫은 $a$가 됩니다.
- 이차식이니 나머지는 일차 이하의 식이 되겠죠.
결론부터 이야기 하자면,
$ \boxed{\text{나머지 일차 이하}}$가 결국 $(x-1)^2$로 나누었을 때 나머지인 $3x + 2$가 되어야 합니다.
아래의 설명으로 원리를 익히고,
다음부터는 나머지를 바로 $ax^2 + bx + c$가 아닌, $(x-1)^2 \cdot a + (3x +2)$로 잡도록 합시다.
일단 $ \boxed{\text{나머지 일차 이하}}$를 모른다 가정하고 문제를 풀어주도록 해주겠습니다.
문제 구조를 확인해 주세요!
$f(x) = (x-1)^2(x+1)Q''(x) + ax^2 + bx + c $ 식에 나머지식을 적용시켜 다시 써줍니다.
$f(x) = (x-1)^2(x+1)Q''(x) + $ $ (x-1)^2 \cdot a + \boxed{\text{나머지 일차 이하}}$
$(x-1)^2$으로 나눈다는 관점에 맞게 정리해주면
$f(x) = (x-1)^2 \left((x+1)Q''(x) + a\right) + \boxed{\text{나머지 일차 이하}}$
$(x-1)^2$으로 나누었을 때 나머지 $ 3x + 2 $ 이므로
$\therefore \boxed{\text{나머지 일차 이하}} = 3x + 2$
결론은
$f(x) = (x-1)^2 \left((x+1)Q''(x) + a\right) + (3x + 2)$
$ax^2 + bx + c$ $= (x-1)^2 \cdot 1 + (3x + 2)$ 가 되는 것이죠!
다음번에는 나머지를 바로 쓸 수 있도록 연습합시다.
남은 풀이를 하도록 할께요.
$f(x) = (x-1)^2 \left((x+1)Q''(x) + a\right) + 3x + 2 $
문제에서 쓰지 않은 남은 조건 $ f(-1) = 3 $을 써줍니다.
$x = -1$ 대입 :
$f(-1) = (-2)^2 \cdot a - 3 + 2$
$3 = 4a - 1$
$\therefore a = 1$
최종 계산 :
$f(x)$를 $(x-1)^2(x+1)$로 나누었을 때 나머지 $ax^2 + bx + c $
$ax^2 + bx + c $
$= (x-1)^2 \cdot a + \text{나머지 일차 이하}$
- $a = 1$이고 나머지는 $3x + 2$ 대입
$= (x-1)^2 \cdot 1 + (3x + 2)$
$= x^2 + x + 3$
이 문제는 대부분 미지수의 개수와 주어진 식의 개수가 맞지 않아 연립으로 미지수의 정확한 값을 구할 수 없을 때 나머지의 일부값만 사용하지 않고 나머지 통째로의 식을 사용해 주는 것입니다.
이 문제로 예를 들면,
$f(x) = (x-1)^2Q(x) + 3x + 2 \quad \dots \quad f(1) = 5$
나머지 $ 3x + 2 $에서 $ x =1 $을 대입한 5의 값만 사용해 주는 것이 아니라 $ 3x + 2 $를 통째로 다 사용해 주는 것이죠.
나머지를 통째로 이용하는 이 문제 풀이는 자주 나오기 때문에 꼭 기억해두시길 바랍니다.
위의 문제풀이 흐름을 따라 계속 연습하다보면 나중에는 나머지를 $ax^2 + bx + c $라고 쓰지 않고 바로 $ (x-1)^2 \cdot a + (3x + 2) $ 이렇게 바로 쓰면서 풀이과정이 생략되고 시간은 줄어들 것이니 처음에는 위의 흐름을 따라 연습하도록 합시다.
개념원리 53p 필수예제08
$f(x) = (x^2 + x - 2)Q(x) + 3x - 2$ → 주어진 식
$f(2x - 3) = (x - 2)Q'(x) + R \quad \Rightarrow \quad f(1) = R$
나머지 $R$ 구해
$\Rightarrow f(1) = R $ 이므로 $f(1)$ 구하는 문제라 생각할 수 있겠네요.
$ \Rightarrow $ 주어진 식의 양변에 $x = 1 $을 대입하면 $ x^2 + x - 2 $가 0이되므로 $Q(x)$ 가 사라집니다.
주어진 식 : $f(x) = (x^2 + x - 2)Q(x) + 3x - 2$
$f(1) = 0 \cdot Q(1) + 1 = R$
$\therefore \quad R = 1$
개념원리 53p 필수예제09
$f(x) = (x-2)Q(x) + 5 \quad \cdots \quad f(2) = 5$
$Q(x) = (x+3)Q'(x) + 3 \quad \cdots \quad Q(-3) = 3$
쓰든 안쓴든 식과 나머지정리의 결론을 항상 둘다 생각하고 식 통째로 쓸지 값만 쓸지 판단해주셔야 합니다.
$f(x) = (x+3)Q''(x) + R \quad \cdots \quad f(-3) = R$
구하고자 하는 것은 $ R = f(-3) $ 입니다.
$f(x) = (x-2)Q(x) + 5 $의 양변에 $x = -3 $ 대입
$f(-3) = -5Q(-3) + 5$
- $ Q(-3) = 3 $이므로
$ f(-3) = -15 + 5$
$ f(-3) = -10 = R$
$\therefore R = -10$
개념원리 54p 필수예제10
문제에서 $ (x-2) $와 $ (x-3) $를 인수로 가진다 하였으므로
$3x^3 + ax^2 + bx + 12 = (x-2)(x-3)Q(x)$
인수정리
$f(a) = 0$
$f(x)$를 $(x-a)$로 나누었을 때 나눈 나머지가 0
$f(x)$를 $(x-a)$로 나누었을 때 나누어떨어진다.
$f(x) = (x-a)Q(x)$
$f(x)$는 $(x-a)$를 인수로 갖는다.
▶풀이 1 ) 수치대입법 이용
$x=2, x=3$을 대입하여 모르는 $Q(x)$를 제거 해주는 풀이 입니다.
- 주어진 식 양변에 $x = 2 $ 대입
$24 + 4a + 2b + 12 = 0$
$\therefore 2a + b = -18$ - 주어진 식 양변에 $x = 3 $ 대입
$81 + 9a + 3b + 12 = 0$
$\therefore 3a + b = -31$
결론의 두 식을 연립해주면,
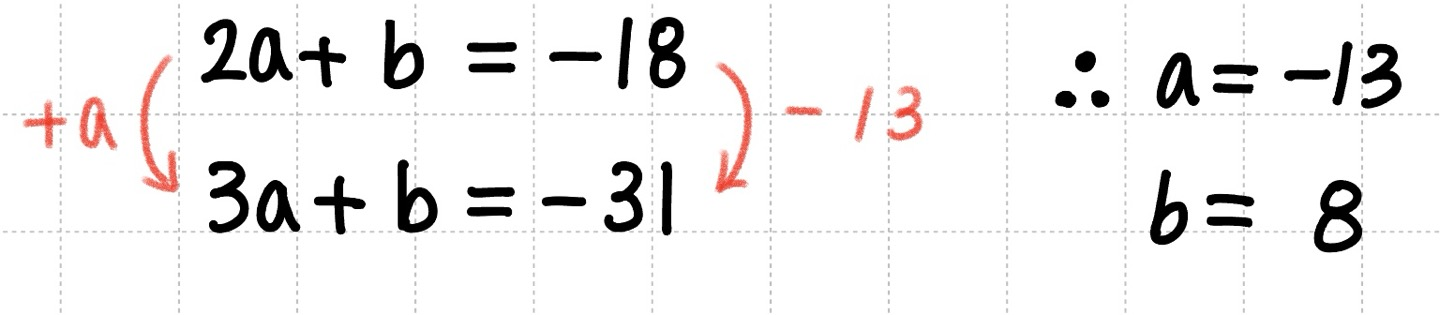
$\therefore a=-13, b = 8$
▶풀이 2 ) $ Q(x) $ 바로 잡고 계수비교법이용
$3x^3 + ax^2 + bx + 12 = (x-2)(x-3)Q(x)$
$ (삼차) = (이차) \cdot (일차) $이므로 $Q(x)$는 일차식 입니다.
최고차계수는 $3x^3$이므로 $Q(x)$의 $x$ 계수, 상수항 12이므로 $Q(x)$ 상수항을 바로 잡으면 $Q(x) = 3x + 2$가 됩니다.

여기서, 계수비교법을 이용해 전개하여 풀수도 있고 아니면 $x^2, x$만 뽑아서 풀어도 됩니다.
<계수비교법 이용>
$ 3x^3 + ax^2 + bx + 12 $
$= (x-2)(x-3)(3x+2)$
$= (x^2 - 5x + 6)(3x + 2)$
$= 3x^3 - 15x^2 + 18x + 2x^2 - 10x + 12$
$= 3x^3 - 13x^2 + 8x + 12$
$\therefore a = -13, b = 8$
< 필요한 계수만 바로 뽑기 >

▶풀이 3 ) 조립제법 이용
$3x^3 + ax^2 + bx + 12 = (x-2)(x-3)Q(x)$

참고:) 혹시나 조립제법을 왜 연달아 해주는지 이해하지 못하겠다면 설명을 읽어주세요.
$3x^3 + ax^2 + bx + 12 = (x-2)(x-3)Q(x)$
- 여기서 $ (x-2) $를 나누는 식으로 보면 몫은 $ (x-3)Q(x) $이고 나머지는 0 입니다.
- $(x-2)$로 나눠 주기 때문에 조립제법의 제일 왼쪽 수는 2가 됩니다.
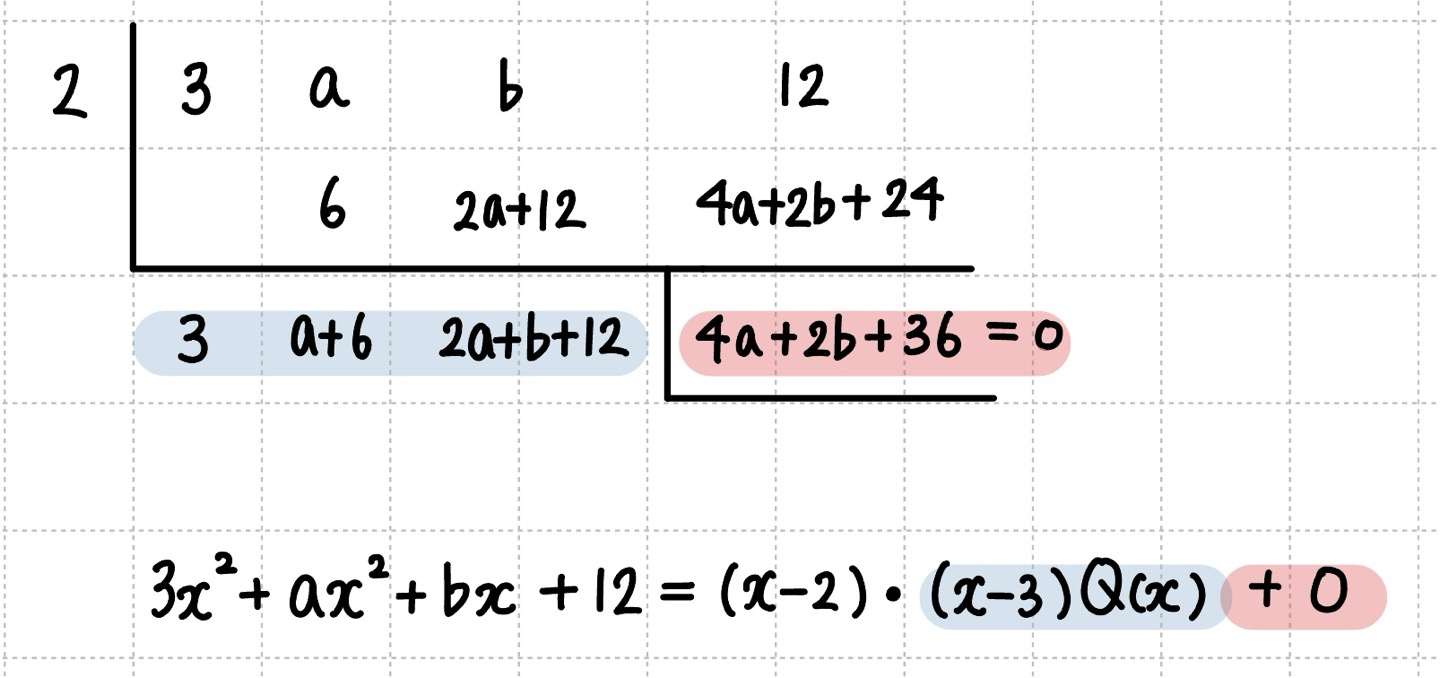
- 조립제법으로 2를 해줬을 때 나온 몫은 $ (x-3)Q(x) $인 것이므로
- 나온 몫을 한번 더 $(x-3)$으로 나누어주면 몫은 $Q(x)$ 나머지는 0이 됩니다.
- $(x-3)$으로 나눠 주기 때문에 조립제법의 제일 왼쪽 수는 3이 됩니다.
이러한 과정으로 연달아 조립제법을 해줄 수 있는 것입니다.
개념원리 54p 필수예제 11번
인수정리
$f(a) = 0$
$f(x)$를 $(x-a)$로 나누었을 때 나눈 나머지가 0
$f(x)$를 $(x-a)$로 나누었을 때 나누어떨어진다.
$f(x) = (x-a)Q(x)$
$f(x)$는 $(x-a)$를 인수로 갖는다.
인수 정리 개념에 의하면,
- 53p 필수예제 10번 문제처럼
$x-2$, $x-3$을 인수로 가진다. → $3x^3 + ax^2 + bx + 12 = (x-2)(x-3)Q(x)$ - 54p 필수예제 11번 문제 처럼
$(x-1)(x+2)$로 나누어 떨어진다. → $x^3 - ax^2 + bx - 2 = (x-1)(x+2)Q(x)$
결국 같은 의미라는 것을 알 수 있겠죠!
$x^3 - ax^2 + bx - 2 = (x-1)(x+2)Q(x)$ 식을 세우고 풀이는 53p 필수예제 10번 처럼 총 3가지의 풀이를 할 수 있습니다.
풀이과정이 아예 같아 이 문제의 풀이는 생략하도록 하겠습니다. 숫자만 바뀐것이나 다름 없으니 위의 풀이를 참고하며 꼭 해보도록 합시다.!!
2. 추가자료
개념 정리 자료 (한글파일 / pdf)
이 파일로 수업내용을 한번 간단하게 핵심 요약 정리를 해보시고 백지테스트를 해보도록 합시다.
"추가로 필요한 자료/ 문제에 대한 다른 풀이방법/ 글을 읽다 궁금한 점은 댓글로 남겨주세요!"
"이 블로그는 개념원리 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."
'공통수학 1 개념' 카테고리의 다른 글
| 공통수학 1 - 1 - 14. 항등식과 나머지 정리 RPM 주요 문제 풀이 (4) | 2025.01.27 |
|---|---|
| 공통수학 1 - 1 - 13. 항등식과 나머지 정리 - 연습문제 풀이 빈출 유형 개념정리 (2) | 2025.01.24 |
| 공통수학 1 - 1 - 11. 항등식과 나머지 정리 - 나머지 정리와 인수정리 (2) | 2025.01.20 |
| 공통수학 1 - 1 - 10. 항등식과 나머지 정리 - 확인체크, 연습문제 풀이 (0) | 2025.01.19 |
| 공통수학 1 - 1 - 9. 항등식과 나머지 정리 - 다항식의 나눗셈과 항등식 (4) | 2025.01.18 |



