
1단원 - 14. 항등식과 나머지 정리 RPM 주요 문제 풀이
이 글에서는 RPM 교재의 항등식과 나머지 정리 주요 문제를 효율적으로 푸는 방법을 제공합니다. 자신의 풀이와 비교해 가며 다양한 풀이를 배우고 주요 유형은 반복 학습을통해 자신의 것으로 꼭 체화시키길 바랍니다.
RPM : 20p ~ 28p
RPM : 29p ~ 31p 풀이는 다음글 1-15에서 설명하도록 하겠습니다.
"모바일 접속 시 함수가 보이지 않을 수 있습니다. 태블릿이나 컴퓨터 또는 chrome(크롬)을 이용해 접속해 주세요."
RPM 22p 127번
'임의의 실수 $x$에 대하여' → $x$에 대한 항등식 입니다.
항등식은 좌변과 우변의 식이 같아야 하고, 어떤 $x$값을 대입해도 =(등호)는 성립하게 됩니다.
풀이1)
나누는 식 $x^2 + x - 1$ 은 인수분해가 되지 않으므로 수치대입법을 이용해 모르는 $Q(x)$를 제거하기 어렵습니다.
그래서 $Q(x)$식을 세워 계수 비교법을 이용해 줘야 합니다.

전개를 해주면,
$x^3 + 0 \cdot x^2 + 5x + a = x^3 + (k+1)x^2 + (k+b-1)x + 3-k$
$k+1 = 0$, $5 = k + b - 1$, $a = 3 - k$
∴ $k = -1$, $b = 7$, $a = 4$
→ $ab = 28$
풀이2)
$x^3 + 5x + a = (x^2 + x - 1)Q(x) + bx + 3$ 에서 $ bx + 3$ 항을 이항시켜줍니다.

직접 나누기 이용하면 정확한 $Q(x)$ 구하기 가능하다는게 눈에 보이시나요 ?!
직접 나누기 방법을 여러번 연습하다보면, 어느 계수가 몫을 정하는 계수인지 알 수 있게 됩니다.
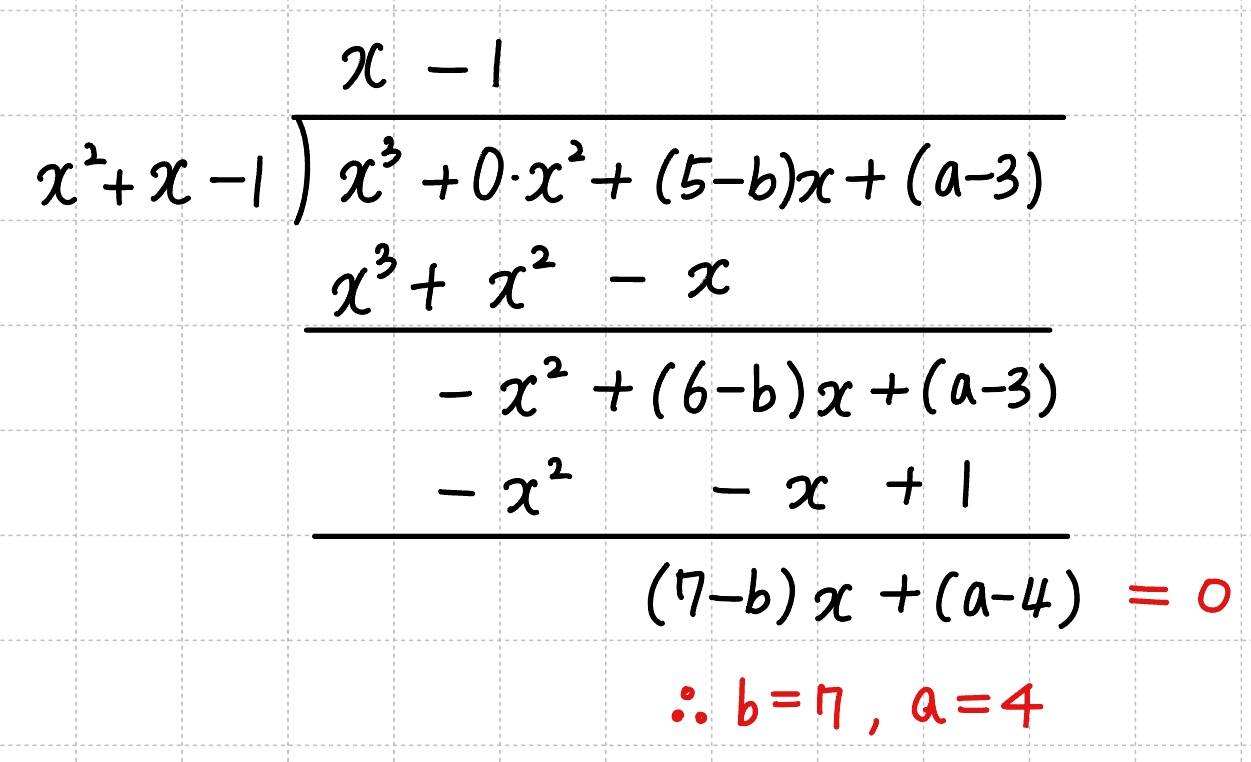
나머지는 0 이므로 $b = 7$, $a = 4$ → $ab = 28$
RPM 22p 129번
모든 실수 $x$에 대하여 → $x$에 대한 항등식 입니다.
전개하여 계수비교법을 이용해 줄 수도 있지만 , 주어진 식을 보면 $(x+2), (x-2)$의 항이 반복되므로 수치대입법을 이용해 줍니다.
- $x = -2$ 대입 → $0 = -16 - 4c$ → ∴ $c = -4$
- $x = 2$ 대입 → $4b = 16 - 4c$ → $4b = 32$ → ∴ $b = 8$
- $x = 0$ 대입 → $-8a + 2b = 0$ → ∴ $a = 2$
∴ $a^2 + b^2 + c^2 = (2)^2 + (8)^2 + (-4)^2 = 4 + 64 + 16 = 84$
추가 풀이:)
항등식은 좌변과 우변의 식이 같아야 합니다. 식의 구조를 이용해서 바로 $a,b,c$의 값을 구할 수도 있습니다.
좌변의 공통되는 $(x+2)$를 묶어주고, 우변의 공통되는 $x^2$을 묶어주면
$(x+2) { a(x+2)(x-2) + b } = x^2(2x-c)$
$(x+2) { ax^2 - 4a + b } = 2x^2 \left(x - \frac{c}{2}\right)$
- 좌변과 우변의 식이 같기 위해 우변에는 $(x+2)$가 있어야하고, 좌변에도 $x^2$이 있어야 합니다.
즉, $ax^2 - 4a + b = 2x^2$, $x + 2 = x - \frac{c}{2}$ 이여야 하므로,
$a = 2$, $b = 8$, $c = -4$
RPM 23p 138번
$x^{50} + 1 = a_{50}(x-1)^{50} + a_{49}(x-1)^{49} + \cdots + a_1(x-1) + a_0$
$a_{\text{홀수}}$들의 합을 구하라고 하였습니다.
- $(x-1) = 1$ 이면 $(x-1)^ {\text{짝수}} = 1$, $(x-1)^{\text{홀수}} = 1$
→ 우변의 $a_{\text{짝수}}$ , $a_{\text{홀수}}$ 앞의 부호 모두 $+$ - $x = 2$ 대입
$2^{50} + 1 = a_{50} + a_{49} + \cdots + a_1 + a_0$
- $(x-1) = -1$ 이면 $(x-1)^ {\text{짝수}} = 1$, $(x-1)^{\text{홀수}} = - 1$
→ 우변에 $a_{\text{짝수}}$ 앞은 $+$, $a_{\text{홀수}}$ 앞은 $-$ - $x = 0$ 대입
$1 = a_{50} - a_{49} + \cdots - a_1 + a_0$
두 식을 연립해주면,

∴ $2^{49} = a_{49} + a_{47} + \cdots + a_1$
RPM 24p 142번
$x^4 + ax^2 + bx = (x^2 - x + 1)Q(x) + 3x - 3$
나누는 식 $x^2 - x + 1$ 은 인수분해가 되지 않으므로 수치대입법을 이용해 모르는 $Q(x)$를 제거 하기 어렵습니다. 그래서 $Q(x)$식을 세워 계수비교법을 이용해 줘야 합니다.
좌변이 4차, 우변의 나누는 식이 2차이므로 몫은 2차가 되어야하는데 , 모르는 항을 미지수 두고 전개해서 계수비교를 해줘도 되지만, 계수들을 비교하여 몫을 바로바로 적어줄 수도 있습니다.
- 좌변의 최고차 계수는 1이므로 몫의 $x^2$의 계수는 1
- 좌변의 $x^3$의 계수는 0 → 우변의 $x^3$ 항은 나누는 식의 $x^2$과 몫의 $x$ 항, 나누는 식의 $x$항과 몫의 $x^2$항이 만나 만들어 집니다.
- 이 둘의 합이 0이 되기 위해 몫의 $x$의 계수가 1이여야 합니다.
- 좌변의 상수항이 3이므로 우변의 나누는 식의 상수항 1과 몫의 상수항이 만나 3이 되야 하므로 몫의 상수항은 3 입니다.

이후 구하고자하는 $x^2$의 계수와 $x$의 계수를 뽑아주고 답을 구해주면 됩니다.
∴ $b - a = (1) - (-3) = 2 $
RPM 26p 158번
$f(x) = (x^2 + x + 1)Q(x) + x + 7$ ... 식①
$Q(x) = (x-1)Q'(x) + 2 \quad \rightarrow \quad Q(1) = 2$ ... 식②
$f(x) = (x^3 - 1)Q''(x) + R(x)$ , $R(x)=?$
나누는 식이 삼차이므로 나머지는 이차이하의 다항식입니다.
주어진 조건과 구해야하는 것을 보면 $ (x^2 + x + 1) $과 $ (x-1) $을 곱하면 $ (x^3 - 1) $이 된다는 것을 알 수 있습니다.
식②의 $Q(x)$에 식① 대입
$f(x) = (x^2 + x + 1)\left((x-1)Q'(x) + 2\right) + x + 7$
$f(x) = (x^2 + x + 1)(x-1)Q'(x) + 2(x^2 + x + 1) + x + 7$
$f(x) = (x^3 - 1)Q'(x) + 2x^2 + 3x + 9$
- $x^3 - 1$을 나누는 식으로 보면 나머지 $2x^2 + 3x + 9 = R(x)$
- 나누는식이 삼차고 나머지가 이차이므로 나누는 식 나머지 관계가 성립한다 할 수 있습니다.
$\therefore R(-3) = 18 - 9 + 9 = 18$
RPM 26p 159번
$x^{2026} + x^{2025} + x = (x-1)Q(x) + R$
몫에대한 언급만 있고, 나머지에 대한 언급이 없다고해서 나머지가 0인것은 아닙니다.
꼭 나머지를 미지수 잡아두고 확인해 주셔야해요.
- 식의 양변에 $x = 1$ 을 대입하면 $3 = R$이므로
$x^{2026} + x^{2025} + x = (x-1)Q(x) + 3$ ... 식①
$Q(x) = (x+1)Q'(x) + R' \quad \Rightarrow \quad Q(-1) = R' = ?$
식①의 양변에 $x = -1$ 대입:)
$1 - 1 - 1 = -2Q(-1) + 3$
$-1 - 3 = -2Q(-1)$
$\therefore Q(-1) = 2 = R'$
RPM 27p 162번
$f(x-2)f(x+1) = (x-2)Q(x)$ : 나누어 떨어진다 하였으므로 나머지는 0 입니다.
$x=2$대입시,
$f(0)f(3) = 0$
$f(0) = 0$ 또는 $f(3) = 0$
$f(x) = x^3 - ax^2 + x - 3$에서 $f(0) = -3 \neq 0$이므로 $f(3) = 0$이어야 합니다.
$\rightarrow f(3) = 27 - 9a = 0$
$\therefore a = 3$
RPM 27p 163번
'${x}^3$의 계수 1인 삼차식 $f(x)$' → $f(x)$에 대한 구체적인 정보가 나왔으므로 $f(x)$ 식세울 준비!
$f(-2) = 2, f(-1) = 2, f(1) = 2$
→ $f(x) = 2$를 만족하는 $x$값: $-2, -1, 1$
→ $f(x) - 2 = 0$을 만족하는 $x$값: $-2, -1, 1$
→ $f(x) - 2$는 $(x+2)(x+1)(x-1)$을 인수로 가짐
'${x}^3$의 계수 1인 삼차식 $f(x)$'
$\therefore f(x) - 2 = 1 \cdot (x+2)(x+1)(x-1)$
$\therefore f(x) = (x+2)(x+1)(x-1) + 2$
$f(x) = (x+3)Q(x) + R$, $R=?$
$f(-3) = R = (-1)(-2)(-4) + 2$
$\therefore R = -6$
RPM 28p 169번
1-9.글의 조립제법과 내림차순 꼴의 항등식에서 추가로 언급했던 문제의 풀이 입니다.
풀이과정은 없었는데 여기서 풀이해보도록 하겠습니다.
$(2x+1)$의 거듭제곱이 반복되는 유형이라 $-\frac{1}{2}$로 연달아 조립제법하면 됩니다.
문제에서 주어진 식을 나누는 식, 몫, 나머지 관점으로 정리하면
- $2x^3 - 3x^2 - 4x + 2 = (2x+1)\left(a(2x+1)^2 + b(2x+1) + c\right) + d$
- 조립제법의 제일 왼쪽수는 $(2x+1)=0$ 되는 $x$값, 즉 $x=-\frac{1}{2}$ 입니다.

- 조립제법 해석시에는 $x$의 계수가 $1$임에 주의해야 합니다.
문제에서는 $(x+\frac{1}{2})$가 아닌 $(2x+1)$의 거듭제곱이 반복됩니다.
문제의 주어진 꼴로 바꾸기 위해 식의 값은 유지한체 변형시켜 줄 것입니다.
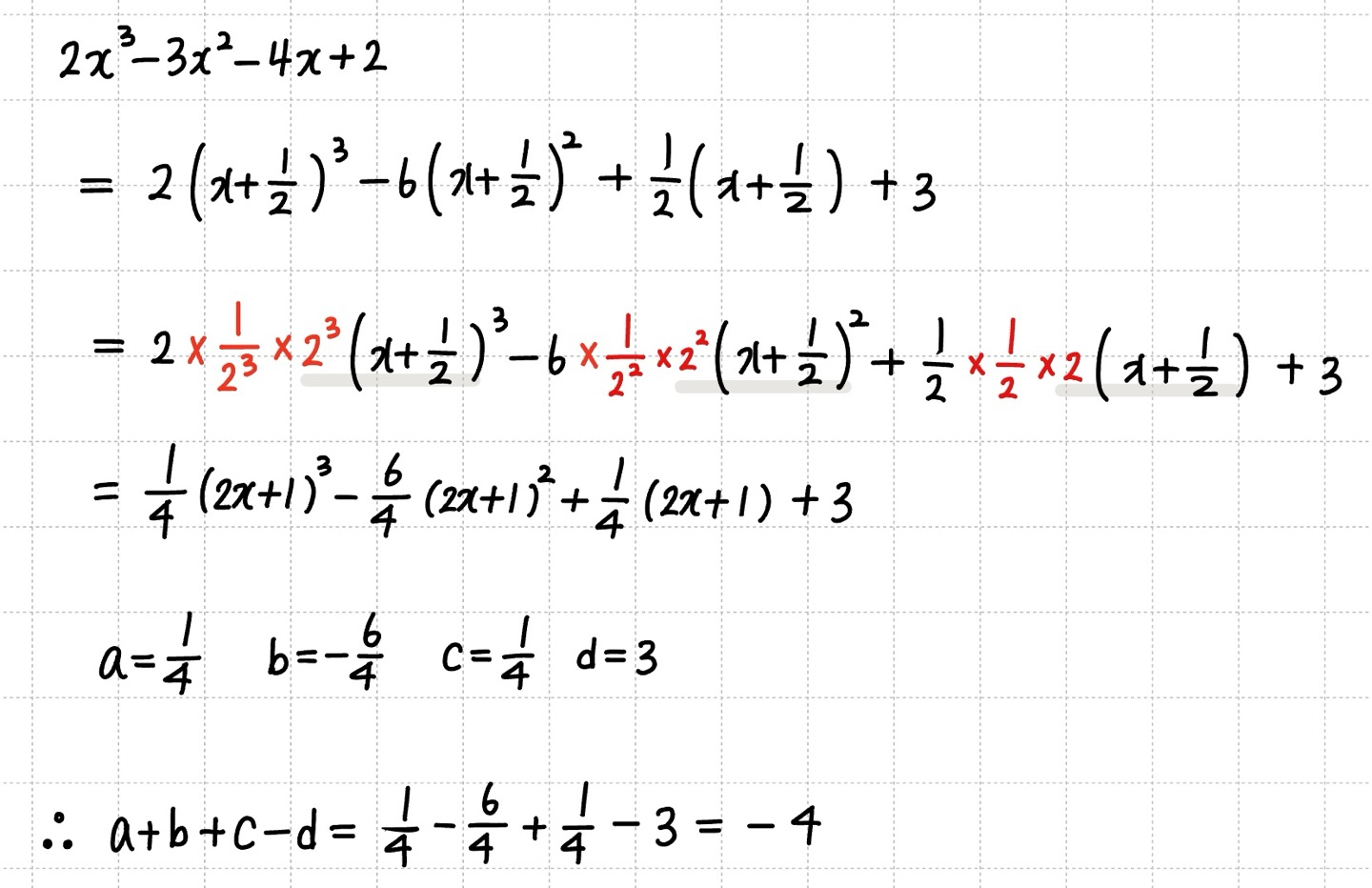
RPM 28p 170번 - 수의 나눗셈에서 나머지 정리의 활용 유형
지난글에서, 수의 나눗셈에서 나머지정리의 활용파트에서 중요한 점 기억나죠?
'수의 나눗셈에서 나머지 정리의 활용 문제유형'에서 주의 해야할 점
1. 나누는 수를 최대한 일차식으로 잡아줌
→ 개념원리 56P 연습문제 115번
2. 최대한 나누는 수를 $x-1$, $x$, $x+1$로 잡아주는 것이 좋음.
→ RPM 30p 188번
3. 마지막에 나누는 수로 나누었을 때 나머지가 성립하는지 확인 : (나누는 수) > (나머지) > 0
→ RPM 28p 170번
3번 경우에 대해 설명하는 문제 입니다.
RPM 24p 170번의 경우 - { " 나누는 수 < 나머지 " 유형 }
RPM 24p 171번의 경우 - { " 나머지가 음수 " 유형 }
두 풀이를 비교해보시길 추천합니다!
{ " 나누는 수 < 나머지 " 유형 }
- $1000 = x$ 라 두면,
$x^{10} = (x-2)Q(x) + R$ - $x = 2$ 대입
$2^{10} = R$ - $\therefore x^{10} = (x-2)Q(x) + 2^{10}$
- $x$에 다시 $1000$을 넣어주고, $2^{10} = 2048$
∴ $1000^{10} = 998 \cdot Q + 2048$
여기서, 나누는 수가 $998$, 나머지 $2048$ 관계는 '나누는수 < 나머지'이므로 성립하지 않습니다. 왜? 한 번 더 나눠져야 하기 때문입니다.
즉, 2048이 998로 또 나눠지게 됩니다. 그래서 한번 더 나눠 보면
$2048 = 998 \cdot 2 + 52$
2048을 998로 나누었을 때 몫은 2, 나머지는 52가 됩니다.
이를 결론식에 넣어 다시 정리해 보면,
$1000^{10} = 998 \cdot Q +$ $998 \cdot 2 + 52$
나누는 수가 998임이 보이도록 묶어주면
$ 1000^{10} = 998 \cdot (Q + 2) + 52$
$1000^{10}$을 998로 나누었을 때 몫 $Q+2$, 나머지 52 : 나누는 수 > 나머지의 관계가 성립하므로 나머지라 할 수 있습니다.
$\therefore$ 나머지는 $52$입니다.
RPM 28p 171번 - 수의 나눗셈에서 나머지 정리의 활용 유형
{ " 나머지가 음수 " 유형 }
- $97 = x$라 두면,
$x^{10} = (x+1)Q(x) + R$ - $x = -1$ 대입
$-1 = R$ - $\therefore x^{10} = (x+1)Q(x) - 1$
- $x = 97$을 다시 넣어주면
∴ $97^{10} = 98Q - 1$
$98로 나누었을 때 나머지-1 관계는 성립하지 않습니다. Why? 한 번 더 나눠졌기 때문이죠.
"한번 더 나눠지는 경우"에 대해 잠깐 공부하고 가도록 할께요.

- 위의 이미지에서 왼쪽 나누기를 보면, 나머지가 제대로 된 것을 알 수 있습니다.
- 그렇다면 오른쪽 나누기를 보면 몫이 4가 아니라 5로 되어있고 나머지가 음수의 값이 나왔습니다.
즉, 원래는 몫이 Q여야 한다면 Q+1로 "한번 더 나눠주었기 때문에 " 나머지가 음수가 나왔고 잘못된 나누기라고 할 수 있는 것이죠.
우리는 이 나누기의 관계를 고등수학에서는 식으로 (가로로) 써서 적어주게 됩니다.
식변형을 통해 올바른 나머지로 고치는 과정이 이미지의 오른쪽 식입니다.
- $9 = 2 \times 5 - 1$ 은 값은 맞지만, 나누는 수- 몫- 나머지 관점에서는 잘못된 식이죠?
- (잘못된 몫) = (원래의 몫) + 1 의 관계 이므로 5 = 4 + 1 로 풀어 적어줍니다.
- 이후 전개하여 정리해주면
- $9 = 2 \times4 + 1$로 나누는 수- 몫- 나머지 관점에서 바른 식으로 정리해 줄 수 있습니다.
이 생각을 문제풀이에 적용시켜보면,
$97^{10} = 98Q - 1$ 의 결론식에서 Q는 잘못된 몫입니다.
- (잘못된 몫) = (원래의 몫) + 1
- Q = (원래의 몫) + 1
- 즉, Q = (Q-1) + 1로 풀어줘야 합니다.
$97^{10} = 98Q - 1$
$97^{10} = 98 \times (Q-1+1) - 1$
$ 97^{10} = 98(Q-1) + 98 - 1$
$ 97^{10} = 98(Q-1) + 97$
$ 97^{10} $을 98로 나누었을 때 나머지는 97로 (나누는 수) > (나머지)의 관계가 성립하므로 ∴나머지=97
"추가로 필요한 자료/ 문제에 대한 다른 풀이방법/ 글을 읽다 궁금한 점은 댓글로 남겨주세요!"
"이 블로그는 개념원리 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."
'공통수학 1 개념' 카테고리의 다른 글
| 공통수학 1 - 1 - 16. 인수분해 - 개념과 공식 정리 예제 문제 (2) | 2025.01.31 |
|---|---|
| 공통수학 1 - 1 - 15. 항등식과 나머지 정리 RPM 주요 문제 풀이 2 (3) | 2025.01.29 |
| 공통수학 1 - 1 - 13. 항등식과 나머지 정리 - 연습문제 풀이 빈출 유형 개념정리 (2) | 2025.01.24 |
| 공통수학 1 - 1 - 12. 항등식과 나머지 정리 - 필수 예제 여러가지 풀이법 (4) | 2025.01.22 |
| 공통수학 1 - 1 - 11. 항등식과 나머지 정리 - 나머지 정리와 인수정리 (2) | 2025.01.20 |



