
2 - 2. 이차방정식
서론 오늘 마지막 남은 이차방정식 특징을 모두 정리해 보도록 할께요 .
이차방정식의 기본 개념부터 근과 계수의 관계, 켤레근 조건, 역수근을 이용한 문제 해결법까지 정리했습니다.
또한, 실전 문제 풀이를 통해 이차방정식의 특징과 응용 전략을 단계별로 설명하며, 특히 근을 활용한 이차방정식 세우기, 실전 꿀팁 공식, 그리고 자주 나오는 유형 총정리로 중간·기말 대비 서술형 및 수능형 문제를 모두 커버할 수 있도록 구성했습니다.
👉 판별식, 완전제곱식, 근의 공식, 역수근 방정식 등 필수 키워드를 중심으로 이 글을 참고하여 수학 개념 이해를 하도록 합시다.
개념원리 공통수학 1 : 119p ~ 120p
"모바일 접속 시 함수가 보이지 않을 수 있습니다. 태블릿이나 컴퓨터 또는 chrome(크롬)을 이용해 접속해 주세요."
1. 이차방정식
이차방정식 글에서 한번 언급하기도 했지만,,
이차방정식 $ax^2 + bx + c = 0$을 푸는 가장 기본적인 방법은 아래와 같습니다.
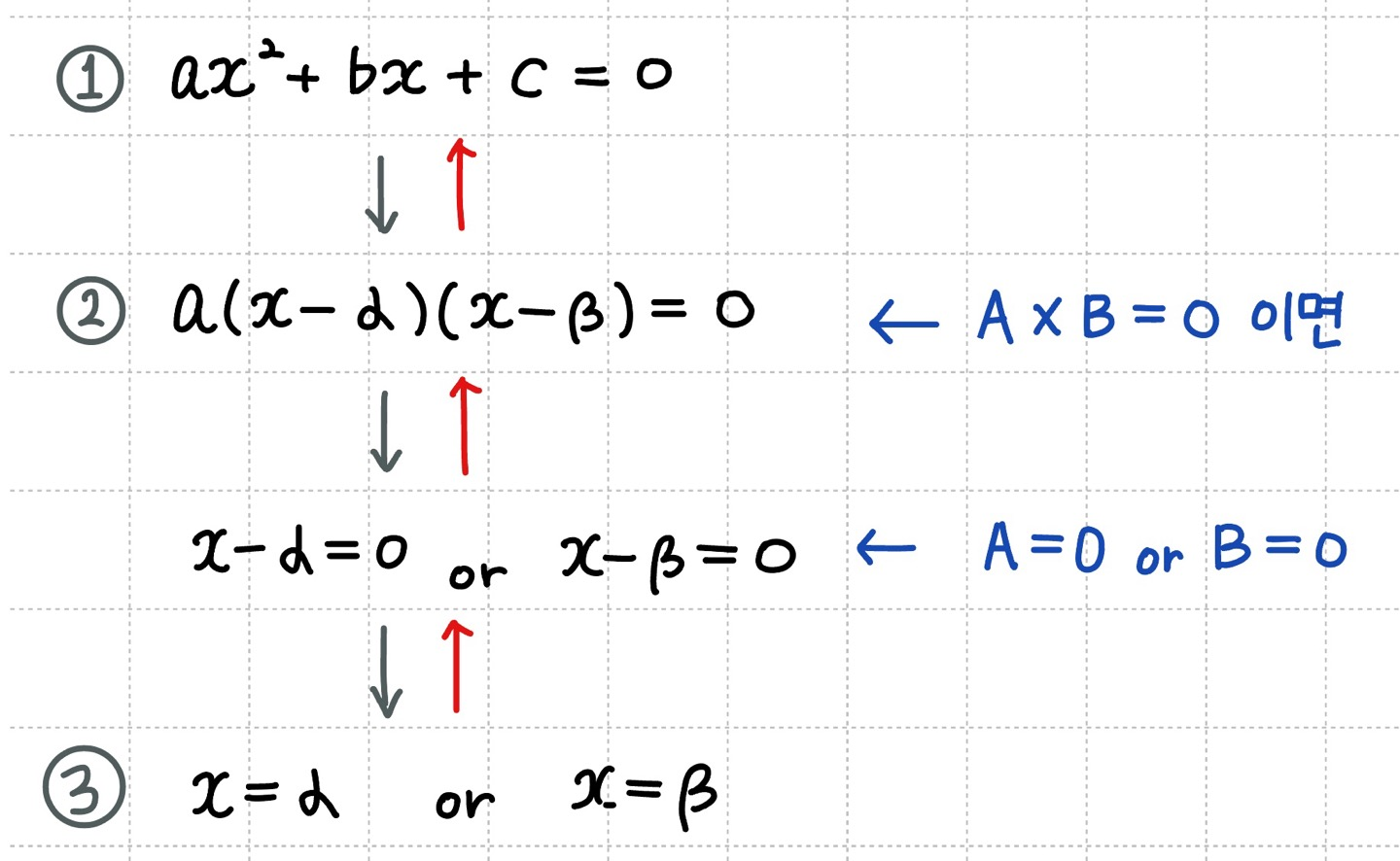
- 이차방정식 $ ax^2 + bx + c = 0 $ 이 $ a(x - \alpha)(x - \beta) = 0 $ 으로 인수분해되면
근은 $ x = \alpha $ 또는 $ x = \beta $ - 이차방정식 $ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면
$ a(x - \alpha)(x - \beta) = 0 $으로 인수분해 됨
📌 간단하게,
1) 이차방정식 $ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ ◀▶ $(x - \alpha)$를 인수로 가진다.
2) 이차방정식 $ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ ◀▶$ a(x - \alpha)(x - \beta) = 0 $으로 인수분해 됨
예:)
이차방정식 $ 1x^2 + 3x + 2 = 0 $ 이 $ 1(x + 1)(x + 2) = 0 $ 으로 인수분해되면 근은 $ x = -1 $ 또는 $ x = -2 $
이차방정식 $ 1x^2 + 3x + 2 = 0 $ 의 근이 $ x = -1 $ 또는 $ x = -2 $이면 $ 1(x + 1)(x + 2) = 0 $ 으로 인수분해 됨
2. 근과 계수의 관계 증명
두가지 방법으로 생각해 볼 수 있습니다.
방법1)
이차방정식 $ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면
$ a(x - \alpha)(x - \beta) = 0 $으로 인수분해 됨
$ a(x - \alpha)(x - \beta) = 0 $
- 다시 전개해 주면,
$ a(x^2 - (\alpha + \beta)x + \alpha \beta) = 0 $
$ ax^2 - a(\alpha + \beta)x + a\alpha \beta = 0 $ ← ( $ = ax^2 + bx + c = 0 $)
(1) $ -a(\alpha + \beta) = b $ → $ \alpha + \beta = -\frac{b}{a} $
(2) $ a\alpha \beta = c $ → $ \alpha \beta = \frac{c}{a} $
이렇게 근과 계수의 관계가 나오게 됩니다.
방법2)
이차방정식 $ ax^2 + bx + c = 0 $ 의 두 근을 근의공식을 이용해 주면,
$ \alpha = \frac{-b + \sqrt{b^2 - 4ac}}{2a} $, $ \beta = \frac{-b - \sqrt{b^2 - 4ac}}{2a} $
($ \alpha, \beta$ 는 임의로 설정)
(1) $ \alpha + \beta$ $= \frac{-b + \sqrt{b^2 - 4ac}}{2a} + \frac{-b - \sqrt{b^2 - 4ac}}{2a} = \frac{-2b}{2a}$ $= -\frac{b}{a} $
(2) $ \alpha \beta$ $= \frac{-b + \sqrt{b^2 - 4ac}}{2a} \times \frac{-b - \sqrt{b^2 - 4ac}}{2a} = \frac{(-b)^2-( \sqrt{b^2 - 4ac} )^2}{4a^2} = \frac{4ac}{4a^2}$ $= \frac{c}{a} $
이렇게 두가지 방법으로 근과 계수의 관계를 생각할 수 있습니다.
저는 많이 사용하지 않는 공식이지만 참고로 아래의 공식을 추가해 놓겠습니다.
$ |\alpha - \beta| = \left| \frac{-b + \sqrt{b^2 - 4ac}}{2a} - \frac{-b - \sqrt{b^2 - 4ac}}{2a} \right| = \left| \frac{2\sqrt{b^2 - 4ac}}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{|a|} $
(단, $ a, \alpha, \beta $ 는 실수이다.)
- 절댓값을 이용해 적어준 이유는 정확하게 $ \frac{-b + \sqrt{b^2 - 4ac}}{2a} $, $ \frac{-b - \sqrt{b^2 - 4ac}}{2a} $ 둘 중 어떤근이 $ \alpha, \beta$인지 모르기 때문에 입니다.
근과 계수의 관계
이차방정식 $ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면
(1) 두근의 합 = $ \alpha + \beta = -\frac{b}{a} $
(2) 두근의 곱 = $ \alpha \beta = \frac{c}{a} $
추가:) $ |\alpha - \beta| = \frac{\sqrt{b^2 - 4ac}}{|a|} $
예)
$ 1x^2 + 3x - 2 = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면
- $ \alpha + \beta = -\frac{3}{1} = -3$
- $ \alpha \beta = \frac{-2}{1} = -2 $
3. 이차방정식 세우기
1. 이차방정식 $ 1x^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면 (최고차항 계수 : 1)
- $ 1(x - \alpha)(x - \beta) = 0 $으로 인수분해 됨
- 전개하면, $ 1x^2 - (\alpha + \beta)x + \alpha \beta = 0 $
두 근의 합에 -를 붙히면 $x$의 계수가 됨 , 두근의 곱이 상수항이 됨
2. 이차방정식 $ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면 (최고차항 계수 : a)
- $ a(x - \alpha)(x - \beta) = 0 $으로 인수분해 됨
- 전개하면, $ ax^2 - a(\alpha + \beta)x + a\alpha \beta = 0 $
두 근의 합에 -를 붙히고 최고차항 계수 곱하면 $x$의 계수가 됨
두근의 곱에 최고차항 계수 곱하면 상수항이 됨
매번 근이 $ x = \alpha $ 또는 $ x = \beta $ 로 주어진 경우
$ a(x - \alpha)(x - \beta) = 0 $로 식을 세우고 직접 전개를 해주셔도 되지만,
근을 보고 바로 식을 $ ax^2 - a(\alpha + \beta)x + a\alpha \beta = 0 $ 세울 수 있으면
조금이나마 문제풀이를 빠르게 할 수 있을 것 같아 구조를 한번 언급했습니다.
예)
최고차항의 계수가 2인 이차방정식의 근이 $ x = 3 $ 또는 $ x = 2 $ 이면
- $2(x-3)(x-2) =0$ 이므로
- 또는
- 두근의 합에 (- 최고차항 계수) 곱하면 : -10 , 두근의 곱에 (최고차항 계수) 곱하면 : 12 이므로
∴$2x^2 - 10x + 12$
4. 이차방정식 켤레근
이차방정식 $ ax^2 + bx + c = 0 $ 의 두 근을 근의공식을 이용해 주면,
$ x = \frac{-b + \sqrt{b^2 - 4ac}}{2a} $ 또는 $ x = \frac{-b - \sqrt{b^2 - 4ac}}{2a} $
이렇게 루트 앞의 부호가 +, - 로 두 근은 항상 켤레 관계를 이용해 만들어 진다는 것을 알 수 있습니다.
이차방정식 $ ax^2 + bx + c = 0 $ 에서
(1) $ a, b, c $ 가 유리수일 때,
한 근이 $ p + q\sqrt{m} $ 이면 다른 한 근은 $ p - q\sqrt{m} $ 이다. ← 루트 앞의 부호 바뀌는 켤레관계
(단, $ p, q $ 는 유리수, $ q \neq 0 $, $ \sqrt{m} $ 은 무리수이다.)
(2) $ a, b, c $ 가 실수일 때,
한 근이 $ p + qi $ 이면 다른 한 근은 $ p - qi $ 이다. ← $i$ 앞의 부호 바뀌는 켤레관계
(단, $ p, q $ 는 실수, $ q \neq 0 $, $ i = \sqrt{-1} $ 이다.)
하지만 계수가 유리수, 실수여야하는 조건이 붙죠 ?
간단한 몇가지 예를 들어보도록 할께요.
(예제1) $ a, b, c $ 가 유리수가 아닌 무리수의 경우
$ a = 1, \quad b = \sqrt{5}, \quad c = 1 $
$ x = \frac{-\sqrt{5} \pm 1}{2} $
$ x = \frac{1}{2} - \sqrt{5} $ 또는 $ x = -\frac{1}{2} - \sqrt{5} $ ← 켤레관계이긴하나 루트 앞의 부호가 바뀌는 것은 아님
(예제 2)$ a, b, c $ 가 실수가 아닌 허수인 경우
$ a = 1, \quad b = 3i, \quad c = -6 $
$ x = \frac{-3i \pm \sqrt{16}}{2} = -\frac{3}{2}i \pm 2 $ ← 켤레관계이긴하나 $i$ 앞의 부호가 바뀌는 것은 아님
(예제 3) 개념원리 107p 필수예제 02 - $ a, b, c $ 가 유리수가 아닌 무리수의 경우
$(\sqrt{2} -1)x^2 - (\sqrt{2} +1)x + 2 = 0$
- 양변에 $(\sqrt{2} +1)$ 을 곱하여
$x^2 - (3+2\sqrt{2})x + 2(\sqrt{2} +1) = 0$
- 근의공식 이용
$x = \frac{3+2\sqrt{2} \pm \sqrt{4\sqrt{2} +9}}{2}$
- $4\sqrt{2} +9 = (2\sqrt{2} +1)^2$ 이므로
$ \pm \frac{\sqrt{4\sqrt{2} +9}}{2} = \pm \frac{\sqrt{(2\sqrt{2} +1)^2}}{2} = \pm \frac{(2\sqrt{2} +1)}{2} $
$x = \frac{3+2\sqrt{2} \pm (2\sqrt{2} +1)}{2}$
즉, $x = 2+2\sqrt{2}$ or $x = 1$ ← 일반적인 켤레 관계의 형태가 아님
예를 들어,
- 이차방정식 $ ax^2 + bx + c = 0 $ 의 한근이 $ 3 + 2\sqrt{7} $
→ 무조건 다른 한근은 $ 3 - 2\sqrt{7} $ 이라 할 수 없음 , 직접 다른 근을 구해봐야 함 - 이차방정식 $ ax^2 + bx + c = 0 $ 의 한근이 $ 3 + 2\sqrt{7} $ , ($a,b,c$는 유리수)
→ 무조건 다른 한근은 $ 3 - 2\sqrt{7} $
이렇게 생각 할 수 있는 것이죠.
5. 역수근을 가지는 이차방정식
$ ax^2 + bx + c = 0 $ 한 근 : $ \alpha $
- $x = \alpha $ 대입시 성립
$ a\alpha^2 + b\alpha + c = 0 $ : 성립
- 양변을 $x = \alpha^2 $ 으로 나눠줘도 식은 성립함
$ c \left(\frac{1}{\alpha}\right)^2 + b \left(\frac{1}{\alpha}\right) + a = 0 $ : 성립
- $ cx^2 + bx + a = 0 $ 에 $x = \frac{1}{\alpha} $ 대입시 성립하는 구조
∴ $ \frac{1}{\alpha} $ 은 $ cx^2 + bx + a = 0 $ 의 근이다.
$(x-a)(x-b)$의 근과 $k(x-a)(x-b)=0$ 의 근은 $x=a$ 또는 $x=b$로 최고차 계수와 관계 없이 근이 같다.
그렇다면,
$ cx^2 + bx + a = 0 $ 과 $ k(cx^2 + bx + a) = 0 $ 의 근도 동일하므로
$ \frac{1}{\alpha} $을 근으로 가지는 이차방정식은 일반화하여 $ k(cx^2 + bx + a) = 0 $
역수근을 가지는 이차방정식
$ ax^2 + bx + c = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $ 이면
$ \frac{1}{\alpha} $, $ \frac{1}{\beta} $ 을 근으로 가지는 이차방정식은 $ k(cx^2 + bx + a) = 0 $ (계수가 반대로 된 꼴)
✅ 삼차, 사차, 오차.. 등의 방정식에서도 동일하게 증명 할 수 있음.
$ ax^4 + bx^3 + cx^2 + dx + e = 0 $ 의 근이 $ \alpha, \beta, \gamma, \lambda $ 이면,
$ \frac{1}{\alpha}, \frac{1}{\beta}, \frac{1}{\gamma}, \frac{1}{\lambda} $ 을 근으로 가지는 사차방정식은
$ k(ex^4 + dx^3 + cx^2 + bx + a) = 0 $
예)
$ 1x^2 + 3x - 2 = 0 $ 의 근이 $ x = \alpha $ 또는 $ x = \beta $
$ \frac{1}{\alpha} + \frac{1}{\beta} $ 의 값은?
- 역수근을 가지는 방정식 개념 이용한 풀이)
$ \frac{1}{\alpha} $, $ \frac{1}{\beta} $ 을 근으로 가지는 이차방정식은 $ k(-2x^2 + 3x + 1) = 0 $
두근의 합 = $ \frac{1}{\alpha} + \frac{1}{\beta} = - \frac{3k}{-2k} = \frac{3}{2} $
이렇게 역수근을 가지는 방정식을 통해 바로 합을 구해 줄 수 있습니다.
- 기본 풀이)
주어진 식의 근과 계수 관계로
- $ \alpha + \beta = -\frac{3}{1} = -3$
- $ \alpha \beta = \frac{-2}{1} = -2 $
이를 이용하여 $ \frac{1}{\alpha} + \frac{1}{\beta} = \frac{ \alpha + \beta }{\alpha \beta} = \frac{-3}{-2} = \frac{3}{2} $
의 풀이도 가능합니다.
6. 추가자료
개념 정리 자료 (한글파일 / pdf)
이 파일로 수업내용을 한번 간단하게 핵심 요약 정리를 해보시고 백지테스트를 해보도록 합시다.
"추가로 필요한 자료/ 문제에 대한 다른 풀이 방법/ 글을 읽다 궁금한 점은 댓글로 남겨주세요!"
"이 블로그는 개념원리 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."
'공통수학 1 개념' 카테고리의 다른 글
| 공통수학 1 - 2 - 18. 이차방정식 확인 체크 풀이와 필수 문제 풀이 모음 (0) | 2025.03.25 |
|---|---|
| 공통수학 1 - 2 - 17. 이차방정식 필수예제 풀이 (0) | 2025.03.22 |
| 공통수학 1 - 2 - 15. 이차방정식 연습문제 step 2,3 (0) | 2025.03.18 |
| 공통수학 1 - 2 - 14. 이차방정식 확인체크 , 연습문제 step1 (0) | 2025.03.15 |
| 공통수학 1 - 2 - 13. 이차방정식의 판별식 (0) | 2025.03.13 |



