
2 - 2. 이차방정식
이차방정식은 수학에서 중요한 개념 중 하나로, 판별식 활용, 근의 공식, 절댓값 방정식 등의 개념을 체계적으로 이해하는 것이 중요합니다. 특히, 최고차 계수가 미지수인 경우 판별식 조건을 설정하는 방법, 절댓값 방정식을 풀기 위한 범위 설정법, 그리고 다양한 풀이 접근법 등을 익히는 것이 문제 해결의 핵심입니다. 이번 글에서는 이차방정식의 필수 개념과 연습문제 풀이법을 정리해 보겠습니다. 이를 통해 학교 시험 및 서술형 대비에 도움을 줄 수 있도록 자세히 설명해 드리겠습니다.
개념원리 공통수학 1 : 75p
"모바일 접속 시 함수가 보이지 않을 수 있습니다. 태블릿이나 컴퓨터 또는 chrome(크롬)을 이용해 접속해 주세요."
1. 필수 확인체크 문제 풀이
개념원리 115p 확인체크 225번
★ ★ '이차'방정식이라 하고 최고차 계수가 미지수인 경우 → $ ( 최고차 계수 ) \neq 0 $ 조건 항상 써주기 ★ ★
이차 방정식 $ (k-1)x^2 ~ $ → $k \neq 1$
서로 다른 두 실근을 갖도록 $\quad D > 0$
- 계수: $\quad a = (k-1), \quad b = 2k, \quad c = k-1$
$x$의 계수가 짝수이므로 $\quad b' = k$ - 판별식 $\quad D/4 = (b')^2 - ac = k^2 - (k-1)(k-1) = 2k -1 > 0$
$\therefore \quad k > \frac{1}{2}$
결론을 정리해 보면, $k \neq 1$, $ k > \frac{1}{2} $
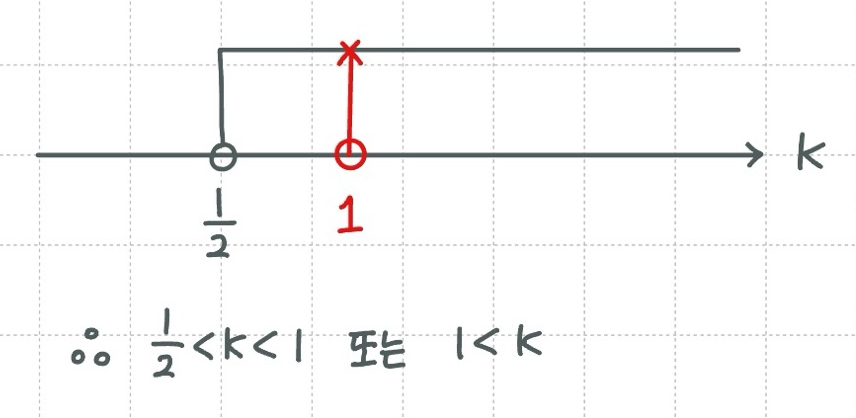
수직선을 해석해 보면,
$\therefore \quad \frac{1}{2} < k < 1 \quad$ 또는 $\quad 1 < k$
개념원리 116p 확인체크 227번
★ ★ '이차'식이라 하고 최고차 계수가 미지수인 경우 → $ ( 최고차 계수 ) \neq 0 $ 조건 항상 써주기 ★ ★
이차식 $ (k-2)x^2 ~ $ → $k \neq 2$
(주어진 식) = 0 인 이차방정식은 (완전제곱식) = 0 으로 중근을 가지므로 $\quad D = 0$
- 계수: $\quad a = (k-2), \quad b = 4(k-2), \quad c = 3k-2$
$x$의 계수가 짝수이므로 $\quad b' = 2(k-2)$ - 판별식 $\quad D/4 = (b')^2 - ac = (2(k-2))^2 - (k-2)(3k-2) = 0$
$k^2 - 8k +12 = 0$
$(k-6)(k-2) = 0$
$\therefore \quad k = 6$ or $k = 2$
결론을 정리해 보면, $k \neq 2$ , $ k = 6 $ or $ k = 2 $
이므로 $\therefore k=6 $
2. 연습문제 step1 풀이 (117p)
개념원리 117p 228번
근의 공식을 이용하여 해를 구해 줍니다.
$x^2 - ax + 7 = 0$
$x = \frac{+a \pm \sqrt{a^2 - 28}}{2(1)}$ $= \frac{5 \pm \sqrt{b} i}{2}$
결론 : $a = 5 , \quad \sqrt{a^2 - 28} = \sqrt{b} i$
- 두번째 식에 $a = 5$ 대입하여 $b$를 구하시면 됩니다.
$\sqrt{-3} = \sqrt{3} i = \sqrt{b} i$ 이므로 $b = 3$
∴ $a=5, b=3, a+b = 8$
참고로,$\sqrt{a^2 - 28} = \sqrt{-(-a^2 + 28)} = \sqrt{-a^2 + 28} i = \sqrt{b} i$
즉, $-a^2 + 28 = b$
가끔 학생들이 $a^2 - 28 = b$ 라고 쓰는 경우가 있어 언급했습니다.
개념원리 117p 229번
한근이 $\alpha$ → 대입시 성립
$2\alpha^2 -2\alpha +1 = 0$
$\alpha^2 - \alpha + \frac{1}{2} = 0$
3가지 방법으로 풀이를 해보도록 하겠습니다.
풀이1) 차수 낮춰주는 풀이
'차수 낮춰주는 풀이'
- 우변에 루트 또는 허수 만 두고 나머지 이항
- 양변 제곱 후 '=0' 으로 정리
- 최고차항 표현 → 상쇄 + 남은 항 → 정리 반복
$\alpha^4 - \alpha^2 + \alpha$
$= \alpha^2 (\alpha^2 - \alpha + \frac{1}{2}) + \alpha^3 - \frac{1}{2} \alpha^2 - \alpha^2 + \alpha$
- 최고차항 $\alpha^4$ 을 $\alpha^2 - \alpha + \frac{1}{2} = 0$ 이용해 표현
- 추가되는 $ - \alpha^3 + \frac{1}{2} \alpha^2 $ 제거 위해 $+ \alpha^3 - \frac{1}{2} \alpha^2$ 추가하여 상쇄
- 남은 항들인 $ - \alpha^2 + \alpha$ 추가
- 정리
$= \alpha^3 - \frac{3}{2} \alpha^2 + \alpha$
- 차수 낮추기 반복
$= \alpha(\alpha^2 - \alpha + \frac{1}{2}) + \alpha^2 - \frac{1}{2} \alpha - \frac{3}{2} \alpha^2 + \alpha$
$= -\frac{1}{2} \alpha^2 + \frac{1}{2} \alpha$
$= -\frac{1}{2} (\alpha^2 - \alpha + \frac{1}{2}) - \frac{1}{2} \alpha + \frac{1}{4} + \frac{1}{2} \alpha$
$= \frac{1}{4}$
∴$\alpha^4 - \alpha^2 + \alpha = \frac{1}{4}$
풀이2) 직접 나누기

∴$\alpha^4 - \alpha^2 + \alpha = \frac{1}{4}$
풀이3) 주어진 조건을 활용
$\alpha^2 - \alpha + \frac{1}{2} = 0$
$\alpha^2 = \alpha - \frac{1}{2}$
$\alpha^4 = \alpha^2 - \alpha + \frac{1}{4}$
$\therefore \alpha^4 - \alpha^2 + \alpha = \frac{1}{4}$
앞전에 공부해봐서 알겠지만, 차수낮추기 풀이로만 풀리던 문제도 있었죠? 가장 간단한 풀이는 세번째 풀이이지만 항상 여러가지 풀이방법을 공부하도록 합시다.
개념원리 117p 232번
조금 독특한 형태로 식이 주어졌고, 절댓값도 존재합니다.
하나하나 차근차근 구해보자면,
- $a * b = 2ab - a - b + 1$
$x * x = 2(x)(x) - x - x + 1 = 2x^2 - 2x + 1$
$1 * x = 2(1)(x) - (1) - (x) + 1 = x$ - $x * x = |1 * x| + 1$
$2x^2 - 2x + 1 = |x| + 1$
절댓값 주어짐 → 범위 나눠주기
1) $x \geq 0$
- $2x^2 - 2x + 1 =$ $(x)$ $+ 1$
$2x^2 - 3x = 0$
$x(2x - 3) = 0$
$\therefore x = 0 \text{ or } x = \frac{3}{2}$ - $x \geq 0$ 범위 만족 최종해 $\therefore x = 0 \text{ or } x = \frac{3}{2}$
2) $x < 0$
- $2x^2 - 2x + 1 =$ $-(x)$ $+ 1$
$2x^2 - x = 0$
$x(2x - 1) = 0$
$\therefore x = 0 \text{ or } x = \frac{1}{2}$ - $x < 0$ 범위 만족 최종해 $\therefore$ 해가 없다
모든 실수 $x$에서 최종해 : $\therefore x = 0 \text{ or } x = \frac{3}{2}$
생각보다 간단하게 풀리니 복잡하게 나왔다고 해서 당황하지 마시고 하나하나 차근차근 !!
"추가로 필요한 자료/ 문제에 대한 다른 풀이 방법/ 글을 읽다 궁금한 점은 댓글로 남겨주세요!"
"이 블로그는 개념원리 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."
'공통수학 1 개념' 카테고리의 다른 글
| 공통수학 1 - 2 - 16. 이차방정식의 근과 계수의 관계 (0) | 2025.03.21 |
|---|---|
| 공통수학 1 - 2 - 15. 이차방정식 연습문제 step 2,3 (0) | 2025.03.18 |
| 공통수학 1 - 2 - 13. 이차방정식의 판별식 (0) | 2025.03.13 |
| 공통수학 1 - 2 - 12. 이차방정식의 활용과 가우스 기호를 포함한 방정식 (2) | 2025.03.11 |
| 공통수학 1 - 2 - 11. 절댓값 기호를 포함한 방정식 (0) | 2025.03.08 |



