
1단원-5.다항식의 연산 - 다항식의 나눗셈
앞서 지난 글에서 다항식의 덧셈과 뺄셈에 대해 배우고, 전개와 곱셈공식을 배우며 곱셈에 관한 내용을 정리했습니다. 이번 글에서는 다항식에서의 나눗셈에 대해 설명해 보려고 합니다. 중학교때는 수에 관해 계산하는 내용을 배웠다면 고등수학에서는 식으로 확장하는게 1단원의 주요 내용입니다. 오늘 내용을 하고 나면 다항식의 사칙 연산을 할 수 있겠네요^^
개념원리 공통수학 1 : 27p ~ 32p
"모바일 접속 시 함수가 보이지 않을 수 있습니다. 태블릿이나 컴퓨터 또는 chrome(크롬)을 이용해 접속해 주세요."
1-1. 다항식의 나눗셈
(다항식) $ \div $ (단항식)

- 수에서 계산
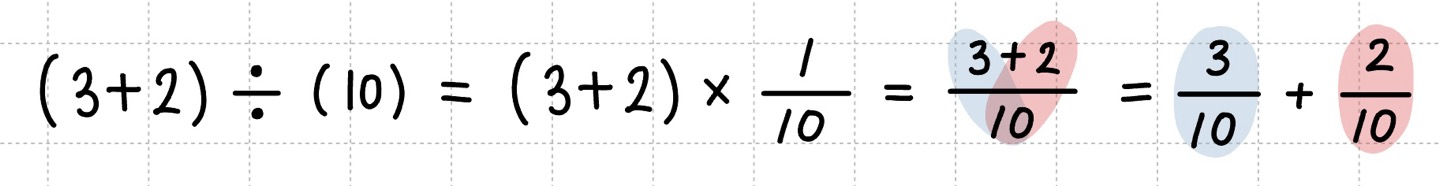
- 식에서 계산

(다항식) $ \div $ (다항식)
수에서와 식에서 직접 나눗셈을 하는 방법입니다.

이렇게 (다항식) $ \div $ (다항식)을 할때는
1. 내림차순으로 정리하고, 계수가 0인 항은 비워 둡니다.
2. 수를 나눌때와 같은 방법으로 계산합니다.
예제를 보면서 직접 나누는 방법에 대해 알아볼께요.
- 예제 : $(4x^3 - 2x^2 - 4) \div (2x^2 - 1)$
1. 내림차순으로 정리하고 계수가 0인 항은 비워 둡니다. ( 이해를 위해 이미지에서는 연한 회색으로 표시해 뒀습니다.)

2. 수를 나눌때와 같은 방법으로 계산합니다.
- $4x^3$을 제거해주기 위해 (나누는 수의 최고차항) $2x^2$과 무엇을 곱하면 될까요 ?
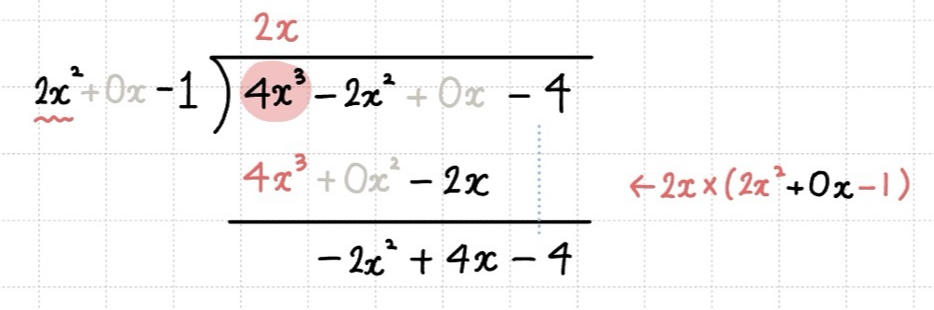
$2x$를 곱하면 되므로 몫의 자리에 $2x$를 적어줍니다. 이 $2x$를 나누는식과 곱한 값을 두번째 줄에 넣고 빼주면 $4x^3$이 사라지고 $ -2x^2 + 4x - 4 $가 남게 됩니다.
- $ -2x^2 $을 제거해주기 위해 (나누는 수의 최고차항) $2x^2$과 무엇을 곱하면 될까요 ?

$-1$를 곱하면 되므로 몫의 자리에 $-1$를 적어줍니다. 이 $-1$를 나누는식과 곱한 값을 두번째 줄에 넣고 빼주면 $-2x^2$이 사라지고 $ 4x - 5 $가 남게 됩니다.
- 이제 , 나누는 식인 $ 2x^2 - 1 $에 어떤 것을 곱해줘도 최소한 2차가 생겨 $ 4x $항을 제거해 줄 수 없으니 여기서 나누기는 끝나게 됩니다. 더 나눌 수 없게 되는 거죠 ! 즉, 몫은 $ 2x - 1 $ 나머지는 $4x - 5$가 됩니다.
이렇게 직접 나누는 방법에 대해서는 익혔고 몇문제만 연습하시다보면 금방 할 수 있을 꺼에요.
1-2. 다항식의 나눗셈에 대한 등식
- 수에서 나누기를 했을 때를 먼저 생각해보겠습니다.

왼쪽과 같이 나누기를 해주면 안된다! 라고 초등학교때 배웠었죠 ? 그렇다면 왜 안될까요 ? 이유는 나머지5가 나누는 수 4로 한번 더 나눠지기 때문입니다. 그래서 (나누는 수) > (나머지) 라고 배웁니다.
$ 9=4 \cdot 1 + 5 $ 는 맞는 식일까요?
- 이식은 왼쪽식의 검산식이기도 합니다.
- 나누기 과정은 틀렸지만 좌변과 우변의 값이 같은 것은 알 수 있습니다. (값 자체로는 등호가 성립하는 맞는 식)
- 하지만, "주어진수 = (나누는 수 ) $ \cdot $ (몫) + 나머지"로 식을 보는 관점에서는 잘못된 식이라고 할 수 있습니다.
- (나누는 수 4 ) < (나머지 5) 이기 때문에 나누기 과정이 틀렸기 때문이지요.
이렇게 식을 어느 관점에서 보냐에 따라 맞는 식일수도 잘못된 식 일 수도 있습니다.
- 다항식에서 나누기를 했을 때를 이제 생각해봅시다.

- 다항식에서도 수에서의 계산과 마찬가지로 끝까지 나눠 줘야 합니다.
- 첫번째 식을 보면 나머지인 $ - x - 3 $을 나누는 수 $ x + 3 $으로 한번 더 나눠 줄 수 있기 때문에 잘못된 나누기입니다.
- 두번째 식의 경우 나머지인 $ 6 $을 나누는 수 $ x + 3 $으로 더이상 나눠 줄 수 없기 때문에 바른 계산 이라고 할 수 있습니다.
다항식에서도 나누기를 하면 수에서 검산을 하듯이 "주어진 식 = (나누는 식) $ \cdot $ (몫) + 나머지" 형태로 식을 나타낼 수 있습니다.
- 첫번째 식의 검산 식을 보면 우변을 전개하여 정리해 주면 좌변과 우변의 식이 같아지면서 등호가 성립한다는 것을 알 수 있습니다. (식 자체는 등호가 성립하여 맞는 식)
- 이 식을 "주어진 식 = (나누는 식) $ \cdot $ (몫) + 나머지" 관점으로 본다면 나누는 식이 $ x + 3 $, 나머지가 $ - x - 3 $으로 한번 더 나눠 줄 수 있기 때문에 잘못된 식이라고 할 수 있습니다.
이렇게 식을 어느 관점에서 보냐에 따라 맞는 식일수도 잘못된 식 일 수도 있습니다.
최종정리를 하도록 해볼께요.
★다항식의 나눗셈에 대한 등식 (검산식)
" (주어진 식) = (나누는 식) $ \cdot $ (몫) + (나머지) " 로 정리 가능
수 : (나누는 식) > (나머지) 를 만족해야함
다항식 : (나누는 식의 차수) > ( 나머지의 차수) 를 만족해야함
고등수학에서는 " (주어진 식) $ \div $ (나누는 식) "을 "(주어진 식) = (나누는 식) $ \cdot $ (몫) + (나머지) " 로 잘 표현합니다. 식을 볼 때 이 관점으로 식을 정리하고 해석하는 것이 목표입니다.

이 식을 "주어진 식 = (나누는 식) $ \cdot $ (몫) + 나머지" 관점으로 보면,

- 나누는 식을 $ x + \frac{b}{a} $ 로 보면, 몫은 $ a \cdot Q(x) $ , 나머지는 $ R $ 입니다.
- 나누는 식을 $ \left(x + \frac{b}{a}\right) \cdot a $ 로 보면, 몫은 $ Q(x) $ , 나머지는 $ R $ 입니다.
이렇게, 어떤 식을 나누는 식으로 보냐에 따라 몫과 나머지는 달라지게 됩니다.
(나누는 식의 차수) > ( 나머지의 차수)만 만족한다면 어느 식을 나누는 식으로 보든 상관 없습니다.
참고 :)
가끔 문제에서 '나누어 떨어진다' 라는 조건이 주어지는데 이는 나머지가 0이라는 뜻입니다.
나머지가 0이라면 $ f(x) $를 온전히 곱꼴로만 나타내어 진다는 뜻이죠. 이에 대해서는 인수분해 단원에서 좀 더 자세하게 배워보도록 하겠습니다.
1-3. 조립제법
: $ f(x) $를 $x$에 대한 일차식으로 나눌 때, 직접 나눗셈을 하지 않고 계수만 이용하여 몫과 나머지를 구하는 방법
일차식으로 나눈 몫, 나머지 둘다 구할 때 쓰는 방법 (주의 : x의 계수가 1인 경우만 사용가능 )
조립제법 방법에 대해 간단히 설명하도록 하겠습니다. 원리에 대해서는 다른글로 다루도록 할께요.
- 예제 : $(x^3 - 5x + 1) \div (x + 2)$ 의 몫과 나머지를 구하시오.
1. 다항식의 계수를 첫 번째 줄에 차례로 적는다. 계수가 $0$인 항은 그 자리에 $0$을 적는다.
ex ) $x^3 - 5x + 1 = 1x^3 + 0x^2 - 5x + 1$ → 1 0 -5 1
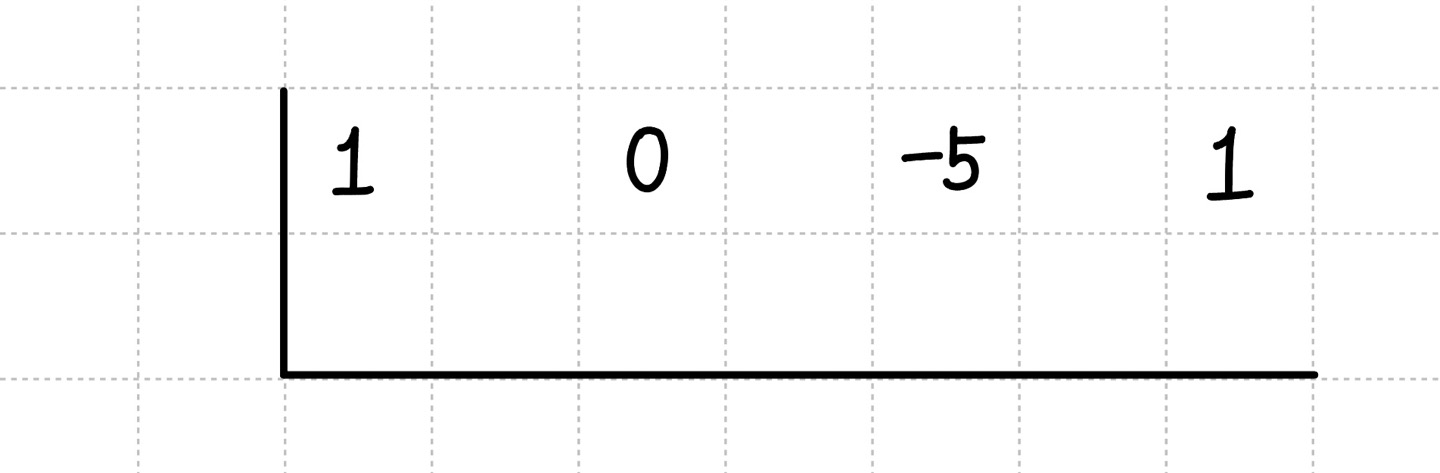
2. (나누는 식) $= 0$이 되는 $x$값을 맨 왼쪽에 적는다.
ex ) $x+2=0$이므로 $x = -2$

3. 최고차항의 계수는 그대로 내려 적는다.

4. 맨 왼쪽에 있는 수 $(1)$과 방금 아래에 적은 수 $(2)$를 곱한 결과를 다음 칸 $(3)$ 에 적고, 위에 있는 수 $(4)$와 합한 값을 더해 $(5)$에 내려 적는다. ( 처음배우면 복잡할 수 있으니 괄호 숫자를 잘보고 따라와 주세요 ! )
→ 대각선은 곱하기 젤 왼쪽 수 , 세로로는 더하기

5. 위의 과정을 반복하며 적는데, 대각선으로는 $x(\text{맨 왼쪽 수})$로 아래로는 더하기를 반복하여 한 칸씩 적는다.
파란색 선은 $x(\text{맨 왼쪽 수})$ , 빨간색 선은 위 아래 수 더하기 !


6. 결론 해석
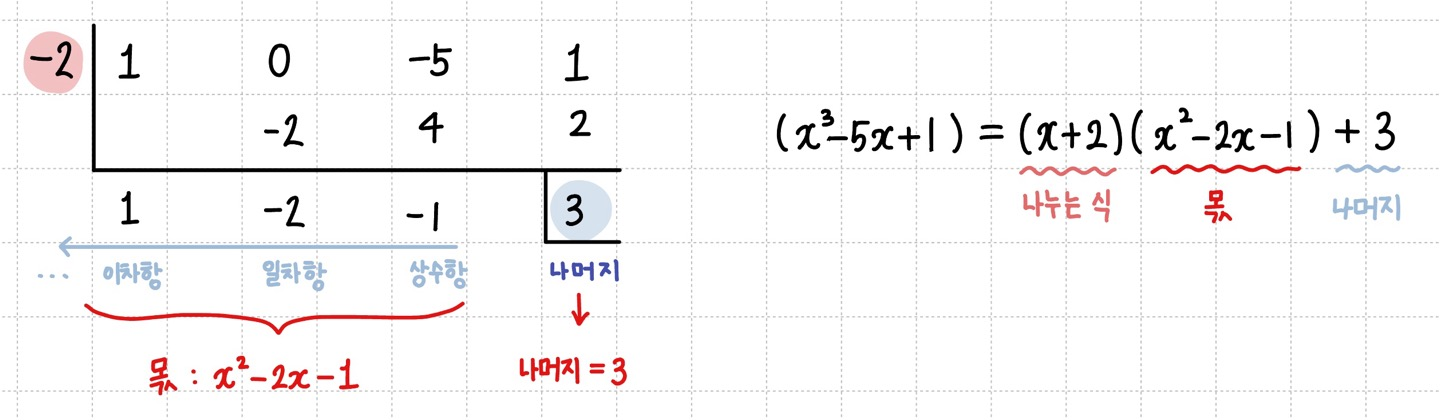
조립제법에서 가장 오른쪽에 있는 수는 나머지가 됩니다. 왼쪽에 있는 수들은 몫의 계수들이 됩니다.
조립제법에서 주의 해야할 점은 $x$의 계수가 1인 일차식으로 나누었을 때 몫과 나머지를 구할 수 있다는 것이에요.
문제가 " $(x^3 - 5x + 1) \div (x + 2)$ 의 몫과 나머지를 구하시오." 였기 때문에 $ (x + 2)$가 나누는 식이라는 것을 알 수 있지만, 조립제법의 결과만 나와있더라도 어떤 식으로 나누는 지 알 수 있어야 합니다.
이와 관련해서 예제를 한개 더 보도록 할께요.
어떤식을 뭐로 나누는지 등에 대한 정보 없이 조립제법의 결과만 나와있습니다.
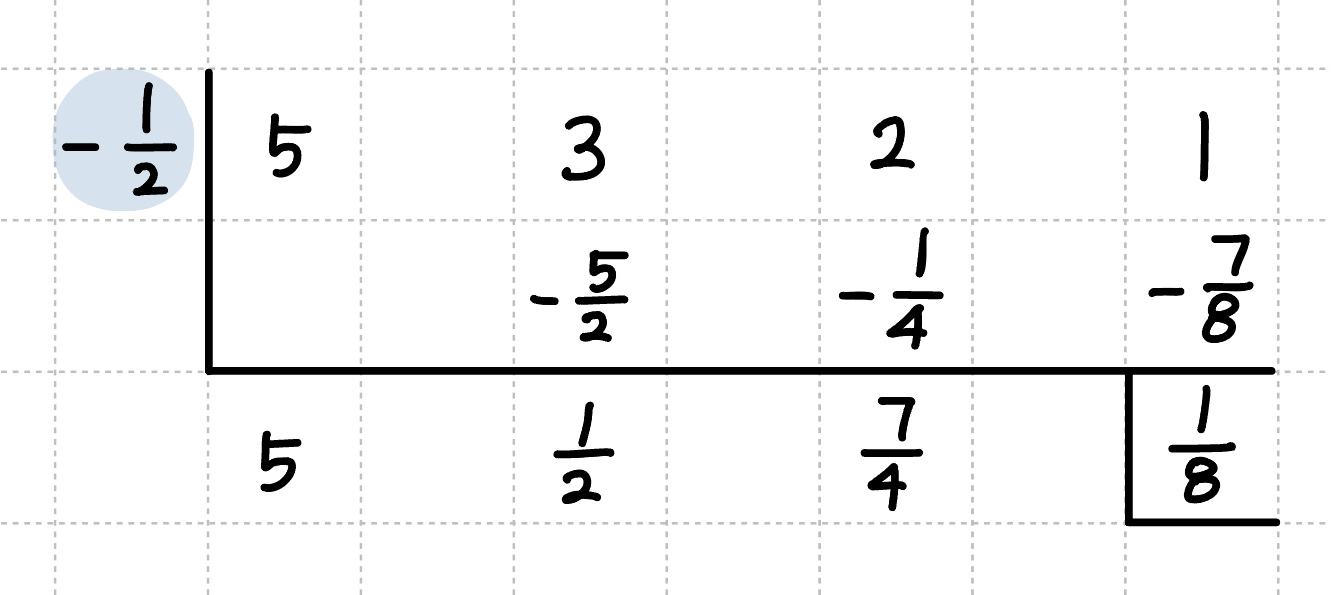
예를 들어, 위와 같은 조립제법 결과가 있다고 생각해 볼께요.
- 맨 왼쪽에 있는 수를 구할 때 (나누는 식) $= 0$이 되는 $x$값 을 구해줬는데, 이 과정을 반대로 해주시면 됩니다.
- 맨 왼쪽에 있는 수가 $-\frac{1}{2}$ 이므로 $x=-\frac{1}{2}$ , $x+\frac{1}{2}=0$ 즉, 나누는 식은 $x+\frac{1}{2}$ 이 됩니다.
- 나누는식은 $x$의 계수가 1인 일차식 입니다. 꼭 기억해 주세요!
- 다항식의 계수도 차례대로 써줬듯이 반대로 차례로 읽어주시면 됩니다.

그렇다면, 조립제법으로 $x$의 계수가 1인 일차식의 몫과 나머지만 구할 수 있을까요? $x$의 계수가 다르다면 조립제법을 사용하지 못하는 걸까요 ?
조립제법을 배우기 직전에 나눗셈의 등식(검산식)은 " (나누는 식의 차수) > ( 나머지의 차수)만 만족한다면 어느 식을 나누는 식으로 보든 상관 없습니다. " 라고 배웠었죠 ? 관점만 바꿔서 생각해주시면 됩니다.
즉, 조립제법 결론에서$(2x + 1)$를 나누는 식으로 보고 싶다면,
- $5x^3 + 3x^2 + 2x + 1 =$ $(x + \frac{1}{2})$ $(5x^2 + \frac{1}{2}x + \frac{7}{4})$ $+ \frac{1}{8}$
- $5x^3 + 3x^2 + 2x + 1 =$ $(x + \frac{1}{2})$ $\cdot 2 \cdot \frac{1}{2} \cdot $ $(5x^2 + \frac{1}{2}x + \frac{7}{4})$ $+ \frac{1}{8}$
- $5x^3 + 3x^2 + 2x + 1 =$ $(2x + 1)$ $ \cdot \frac{1}{2} \cdot $ $(5x^2 + \frac{1}{2}x + \frac{7}{4})$ $+ \frac{1}{8}$
이렇게 나누는 식의 관점을 바꾸기 위해 식의 값은 유지한체 변형해주면 됩니다.
$(2x + 1)$ 를 나누는 식으로 보면, 몫은 $ \frac{1}{2} \cdot $ $(5x^2 + \frac{1}{2}x + \frac{7}{4})$ , 나머지는 $+ \frac{1}{8}$
1-4. 예제 문제
문제를 보면서 배웠던 개념을 복습해 보도록 합시다.
설명할 문제 : 개념원리 31 p 필수예제 13, 개념원리 31p 필수예제 14, 개념원리 32p 필수예제 15 (2)
개념원리 31 p 필수예제 13
문제에서 다항식을 뭐로 나누었을 때 몫이~ 나머지가~ 이런 설명이 있으면 바로 식으로 적어주면서 읽어 주세요.

이후 나머지를 이항해서 정리 해 줍니다.
$x^4 - 3x^2 - 8x - 15 = A \cdot (x^2 + x + 3)$
- 여기서 나누는 식은 A , 몫은 $(x^2 + x + 3)$ 입니다.
$x^4 - 3x^2 - 8x - 15 = (x^2 + x + 3) \cdot A $
- 곱하기는 자리 바꿔도 상관없으니 이렇게 식을 보면, 나누는 식은 $(x^2 + x + 3)$, 몫은 A입니다.
직접 나누기를 이용하여 A를 구해 볼께요.
cf) $A = (x^4 - 3x^2 - 8x - 15) \div (x^2 + x + 3)$ 처럼 한번 더 이항해서 A=으로 정리해 생각해셔도 됩니다.

줄맞춰 적어주고, 계수가 0인 항은 꼭 비워서 적어줘야 합니다.
개념원리 31p 필수예제 14
문제에서 다항식을 뭐로 나누었을 때 몫이~ 나머지가~ 이런 설명이 있으면 바로 식으로 적어주면서 읽어 주세요.
$f(x) = (x - \frac{2}{3}) Q(x) + R$
그런데, 문제에서 $(3x - 2)$로 나누었을 때의 몫과 나머지를 구하라고 하였습니다.
식의 값은 유지한체 $(3x - 2)$로 나누었을 때의 관점으로 식을 변형해 볼께요.
- $f(x) = (x - \frac{2}{3}) Q(x) + R$
- $f(x) = (x - \frac{2}{3}) \cdot 3 \cdot \frac{1}{3} \cdot $ Q(x) + R$
- $f(x) = (3x - 2) \cdot \frac{1}{3} \cdot Q(x) + R$
나누는 식을 $(3x - 2)$ 로 보면, 몫은 $ \frac{1}{3} \cdot Q(x) $ , 나머지는 $ + R$ 입니다.
나누는 식의 차수가 일차고 나머지가 상수항이므로 $(3x - 2)$를 나누는 식으로 보는 것이 가능합니다.
이렇게 관점을 바꿀 때는 나누는 식의 차수와 나머지의 차수를 꼭 확인 해 주세요.
$\therefore \text{몫} = \frac{1}{3} Q(x), \text{나머지} = R$
개념원리 32p 필수예제 15 (2)
나누는 식의 $x$의 계수가 2인데, 조립제법을 이용해서 몫과 나머지를 구해볼께요.

일단, (나누는 식)=0 되는 $x$ 값을 제일 왼쪽에 써주고 조립제법을 해줍니다.
조립제법을 해석 할때는 $x$의 계수가 1이라고 해석을 해야 하기 때문에, 조립제법 해석의 결과를 먼저 써줍니다.

이후, 문제에서는 $(2x-3)$으로 나누는 식을 보라고 하였기 때문에, 식의 값은 유지한체 관점을 변형시켜 줍니다.

$\therefore , \text{몫} = (x^2 - x + 1), , \text{나머지} = 6$
이렇게, $x$의 계수가 1이 아닌 다른 수 일때 조립제법을 사용시 해석할때는 $x$의 계수를 1로 해석하고 관점을 변형시켜주는 풀이를 해야합니다.
이렇게 식을 볼때 관점에 따라 식을 변형 시킬 수 있고, 나눗셈의 등식은 응용문제가 매우많고 뒤에 항등식단원에서도 계속계속 나올 내용이기 때문에 오늘 공부한 내용이 조금 어렵더라도 정확히 이해하고 항등식 단원을 공부하시길 바랍니다!
1-5. 추가자료
개념 정리 자료 ( 한글파일 / pdf)
이 파일로 수업내용을 한번 간단하게 핵심 요약 정리를 해보시고 백지 테스트를 해보도록 합시다.
"추가로 필요한 자료/ 문제에 대한 다른 풀이 방법/ 글을 읽다 궁금한 점은 댓글로 남겨주세요!"
"이 블로그는 개념원리 교재를 참고하여 학습 내용을 정리하였으며, 저작권 보호를 위해 원문 문제는 제공하지 않고 제 풀이와 학습 팁을 중심으로 구성하여 독창적인 풀이와 함께 효율적인 학습 방법을 공유합니다."
'공통수학 1 개념' 카테고리의 다른 글
| 공통수학 1 - 1 - 7. 다항식의 연산 RPM 주요 문제 풀이 (4) | 2025.01.13 |
|---|---|
| 공통수학 1 -1 - 6. 다항식의 연산 확인체크 - 연습문제 풀이 (2) | 2025.01.11 |
| 공통수학 1 -1 - 4. 다항식의 연산 - 곱셈 공식의 변형 (4) | 2025.01.07 |
| 공통수학 1 - 1 - 3. 다항식의 연산 - 곱셈 공식 증명 유도와 예제 문제 풀이 (2) | 2025.01.06 |
| 공통수학 1 - 1 - 2. 다항식의 연산 - 지수 법칙과 다항식의 곱셈 (4) | 2025.01.02 |



